题目内容
【题目】已知y是x的函数，自变量x的取值范围是x≠0的全体实数，如表是y与x的几组对应值．
x | … | ﹣3 | ﹣2 | ﹣1 | ﹣ | ﹣ |
|
| 1 | 2 | 3 | … |
y | … |
|
| ﹣ | ﹣ | ﹣ |
|
|
| m |
| … |
小华根据学习函数的经验，利用上述表格所反映出的y与x之间的变化规律，对该函数的图象与性质进行了探究．下面是小华的探究过程，请补充完整：
（1）从表格中读出，当自变量是﹣2时，函数值是 ；
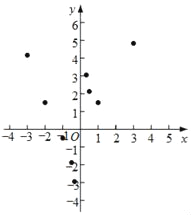
（2）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（3）在画出的函数图象上标出x＝2时所对应的点，并写出m＝ ．
（4）结合函数的图象，写出该函数的一条性质： ．
【答案】（1）
，（2）见解析，（3）见解析，
，（4）当0＜x＜1时，y随x的增大而减小．
【解析】
（1）根据表中x，y的对应值即可得到结论；
（2）按照自变量由小到大，利用平滑的曲线连结各点即可；
（3）在所画的函数图象上找出自变量为2所对应的函数值即可；
（4）利用函数图象的图象求解．
（1）当自变量是﹣2时，函数值是；
故答案为：
（2）该函数的图象如图所示；
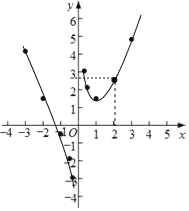
（3）当x＝2时所对应的点 如图所示，且m＝；
故答案为：；
（4）函数的性质：当0＜x＜1时，y随x的增大而减小．
故答案为：当0＜x＜1时，y随x的增大而减小．
【题目】每个人都应怀有对水的敬畏之心，从点滴做起，节水、爱水，保护我们生活的美好世界．某地近年来持续干旱，为倡导节约用水，该地采用了“阶梯水价”计费方法，具体方法：每户每月用水量不超过4吨的每吨2元；超过4吨而不超过6吨的，超出4吨的部分每吨4元；超过6吨的，超出6吨的部分每吨6元．该地一家庭记录了去年12个月的月用水量如下表，下列关于用水量的统计量不会发生改变的是（ ）
用水量x（吨） | 3 | 4 | 5 | 6 | 7 |
频数 | 1 | 2 | 5 | 4﹣x | x |
A. 平均数、中位数 B. 众数、中位数 C. 平均数、方差 D. 众数、方差
