题目内容
【题目】如图,四边形![]() 是菱形,
是菱形,![]() 分别是
分别是![]() 上的动点,连接
上的动点,连接![]() ,则
,则![]() 的最小值为__________.
的最小值为__________.

【答案】![]()
【解析】
连接BQ、PB,由菱形的对角线互相垂直平分,可得B. D关于AC对称,则PB=PD,可知当B、P、Q共线时PQ+PD=PQ+BP=BQ最小,BQ为所求,当BQ⊥AD时,BQ最小,继而利用面积法求出BQ长即可得答案.
连接BQ、PB,
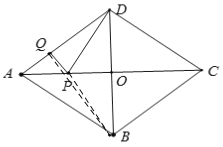
由菱形的对角线互相垂直平分,可得B. D关于AC对称,则PB=PD,
∴PQ+PD=PQ+BP,
则当B、P、Q共线时PQ+PD=PQ+BP=BQ最小,BQ为所求,当BQ⊥AD时,BQ最小,
∵四边形ABCD是菱形,AC=8,DB=6,
∴OA=4,OB=3,AC⊥BD,
在Rt△AOB中,AB=![]() =5,
=5,
∵S菱形ABCD=![]() ,
,
∴![]() ,
,
∴BQ=![]() ,
,
∴DP+PQ的最小值为![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】某学校抽查了某班级某月10天的用电量,数据如下表:
用电量/度 | 8 | 9 | 10 | 13 | 14 | 15 |
天数 | 1 | 1 | 2 | 3 | 1 | 2 |
(1)这10天用电量的众数是______度,中位数是______度;
(2)求这个班级平均每天的用电量;
(3)该校共有20个班级,该月共计30天,试估计该校该月总的用电量.