题目内容
【题目】如图,等边三角形ABC中,E是线段AC上一点,F是BC延长线上一点.连接BE,AF.点G是线段BE的中点,BN∥AC,BN与AG延长线交于点N.
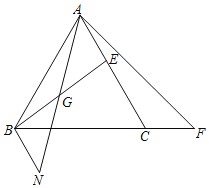
(1)若∠BAN=15°,求∠N;
(2)若AE=CF,求证:2AG=AF.
【答案】(1)45°;(2)见解析
【解析】
(1)由等边三角形的性质可知∠ABC=∠ACB=60°,由平行线的性质可知∠NBC=60°,进一步求出∠ABN=120°,再由三角形内角和定理即可求出∠N的度数;
(2)先证△NBG≌△AEG,得到AG=NG,AE=BN,再证△ABN≌△ACF,即可推出AF=2AG.
解:(1)∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵AC∥BN,
∴∠NBC=∠ACB=60°,
∴∠ABN=∠ABC+∠NBC=120°,
∴在△ABN中,
∠N=180°﹣∠ABN﹣∠BAN=180°﹣120°﹣15°=45°;
(2)∵AC∥BN,
∴∠N=∠GAE,∠NBG=∠AEG,
又∵点G是线段BE的中点,
∴BG=EG,
∴△NBG≌△AEG(AAS),
∴AG=NG,AE=BN,
∵AE=CF,
∴BN=CF,
∵∠ACB=60°,
∴∠ACF=180°﹣∠ACB=120°,
∴∠ABN=∠ACF,
又∵AB=AC,
∴△ABN≌△ACF(SAS),
∴AF=AN,
∵AG=NG=![]() AN,
AN,
∴AF=2AG.

练习册系列答案
相关题目