题目内容
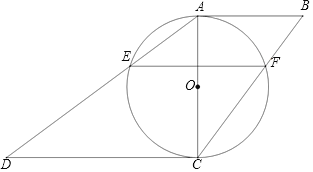
【题目】如图,在四边形ABCD中,AB∥CD,以AC为直径的⊙O交AD于点E,交BC于点F,AB2=BFBC.
(1)求证:AB与⊙O相切;
(2)若![]() .
.
①求证:AC2=ABCD;
②若AC=3,EF=2,则AB+CD= .
【答案】(1)证明见解析;(2)①证明见解析;②9.
【解析】
(1)连接AF,由题意可证△ABC∽△FBA,可得∠BAC=∠BFA=∠AFC=90°,由切线的判定可得AB与⊙O相切;
(2)①通过证明△ABC∽△CAD,可得![]() ,可得AC2=AB·CD;
,可得AC2=AB·CD;
②由垂径定理和勾股定理可求OG的长,由平行线分线段成比例求出AB的长,代入AC2=AB·CD,可求CD的长,即可求AB+CD的值.
(1)连接AF,

∵AC是⊙O的直径,
∴∠AFC=∠AFC =90°
∵AB2=BF·BC,
即![]() ,且∠B=∠B,
,且∠B=∠B,
∴△ABC∽△FBA,
∴∠BAC=∠BFA=90°,
即OA⊥AB,
且∵点A在⊙O上,
∴AB与⊙O相切
(2)①连接CE,

∵![]() ,AC是⊙O的直径,
,AC是⊙O的直径,
∴![]() ,
,
∴AE=AF,CE=CF,
∴AC垂直平分EF.
∵AB//CD,
∴∠ACD=∠CAB=∠AGE=90°,
∴EF//CD,
∴∠AEF=∠D.
∵∠AEF=∠ACB,
∴∠ACB=∠D,且∠ACD=∠CAB,
∴△ABC∽△CAD,
∴![]() ,
,
∴AC 2=AB·CD
②连接OF

∵OG⊥EF,
∴GF![]() EF=1,
EF=1,
∴OG![]() ,
,
∴CG![]()
∵EF//AB,
∴![]() ,
,
∴AB![]()
∵AC 2=AB·CD,
∴AC![]() ,
,
∴AB+CD=9
故答案为:9.

【题目】如图,点P是以O为圆心,AB为直径的半圆上的动点,AB=6cm,设弦AP的长为xcm,△APO的面积为ycm2,(当点P与点A或点B重合时,y的值为0).小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小明的探究过程,请补充完整;
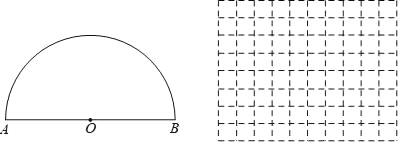
(1)通过取点、画图、测量、计算,得到了x与y的几组值,如下表:
x/cm | 0.5 | 1 | 2 | 3 | 3.5 | 4 | 5 | 5.5 | 5.8 |
y/cm2 | 0.8 | 1.5 | 2.8 | 3.9 | 4.2 | m | 4.2 | 3.3 | 2.3 |
那么m= ;(保留一位小数)
(2)建立平面直角坐标系,描出以表中各组对应值为坐标的点,画出该函数图象.
(3)结合函数图象说明,当△APO的面积是4时,则AP的值约为 .(保留一位小数)
【题目】为迎接2022年冬奥会,鼓励更多的学生参与到志愿服务中来,甲、乙两所学校组织了志愿服务团队选拔活动.为了了解两所学校学生的整体情况,从两校进入综合素质展示环节的学生中分别随机抽取了50名学生的综合素质展示成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
a.甲学校学生成绩的频数分布直方图如图:

b.甲学校学生成绩在80~90这一组的是:
80 | 80 | 81 | 81 | 82 | 82 | 83 | 83 |
85 | 86 | 86 | 87 | 88 | 88 | 89 | 89 |
c.乙学校学生成绩的平均数、中位数、众数、优秀率(85分及以上为优秀)如下:
平均数 | 中位数 | 众数 | 优秀率 |
85 | 84 | 78 | 46% |
根据以上信息,回答下列问题:
(1)甲学校学生成绩的中位数为 分;
(2)甲学校学生A、乙学校学生B的综合素质展示成绩同为83分,这两人在本校学生中的综合素质展示排名更靠前的是 (填“A”或“B”);
(3)根据上述信息,推断哪所学校综合素质展示的水平更高,并至少从两个不同的角度说明推断的合理性.
【题目】某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
(1)这天部分出行学生使用共享单车次数的中位数是 ,众数是 .
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少名.