Question

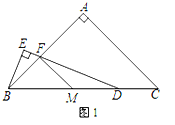
【题目】如图,已知点M是△ABC的边BC的中点,点O是△ABC外一点.

（1）画△A'B'C',使△A'B'C'与△ABC关于点M成中心对称;
（2）画△A″B″C″,使△A″B″C″与△ABC关于点O成中心对称.

Answer 1

【答案】
（1）解：①连接AM并延长至A',使MA'=AM;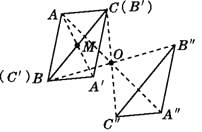

②点B关于点M的对称点B'即为点C,点C关于点M的对称点C'即为点B;
③连接A'B',A'C',则△A'B'C'即为所求.
（2）解：①连接AO,BO,CO,并分别延长至A″,B″,C″,
使OA″=AO,OB″=BO,OC″=CO;
②连接A″B″,A″C″,B″C″,则△A″B″C″即为所求
【解析】（1）先找出点A、B、C关于点M的对称点A′、B′、C′，再将点A′、B′、C′顺次连接即可。
（2）先找出点A、B、C关于点O的对称点A″、B″、C″，再将点A″、B″、C″顺次连接即可。