题目内容
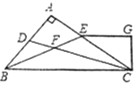
【题目】如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG//BC,且![]() 于G,下列结论:①
于G,下列结论:①![]() ;②
;②![]() 平分
平分![]() ;③
;③![]() ;④
;④![]() ;其中正确的结论是( )
;其中正确的结论是( )
A.只有①③B.只有①③④C.只有②④D.①②③④
【答案】B
【解析】
根据平行线、角平分线、垂直的性质及三角形内角和定理依次判断即可得出答案.
①∵EG∥BC,
∴∠CEG=∠ACB,
又∵CD是△ABC的角平分线,
∴∠CEG=∠ACB=2∠DCB,故本选项正确;
②无法证明CA平分∠BCG,故本选项错误;
③∵∠A=90°,
∴∠ADC+∠ACD=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴∠ADC+∠BCD=90°.
∵EG∥BC,且CG⊥EG,
∴∠GCB=90°,即∠GCD+∠BCD=90°,
∴∠ADC=∠GCD,故本选项正确;
④∵∠EBC+∠ACB=∠AEB,∠DCB+∠ABC=∠ADC,
∴∠AEB+∠ADC=90°+![]() (∠ABC+∠ACB)=135°,
(∠ABC+∠ACB)=135°,
∴∠DFE=360°135°90°=135°,
∴![]() ,故本选项正确.
,故本选项正确.
故选:B.

练习册系列答案
相关题目