Question

【题目】如图，线段AC∥x轴，点B在第四象限，AO平分∠BAC，AB交x轴于G，连OB，OC．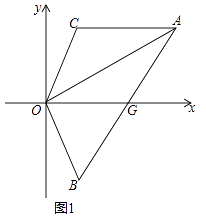

（1）判断△AOG的形状，并证明；
（2）如图1，若BO=CO且OG平分∠BOC，求证：OA⊥OB；
（3）如图2，在（2）的条件下，点M为AO上的一点，且∠ACM=45°，若点B（1，﹣2），求M的坐标．

Answer 1

【答案】
（1）

解：∵AO平分∠BAC，

∴∠CAO=∠BAO，

∵线段AC∥x轴，

∴∠CAO=∠AOG，

∴∠BAO=∠AOG，

∴GO=GA，

∴△AOG是等腰三角形

（2）

解：如图1，

连接BC，

∵BO=CO且OG平分∠BOC，

∴BF=CF，

∵线段AC∥x轴，

∴AG=BG，

由（1）得OG=AG，

∴OG= AB，

∴△AOB是直角三角形，

∴OA⊥OB，

（3）

解：如图2，连接BC，

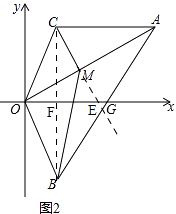
由（2）有，BF=CF，BC⊥OG，

∵点B（1，﹣2），

∴BF=2，OF=1，

在Rt△BFG中，BF=2，BG=FG+1，

根据勾股定理得，（FG+1）2=FG2+4，

∴FG= ，

∵AC∥OG，AG=BG，

∴AC=2FG=3，

由（2）有，BF=CF，BC⊥OG，

∵点B（1，﹣2），

∴C（1，2），A（4，2），

∴直线OA解析式为y= x①，

延长CM交x轴于E，

∵∠ACM=45°，

∴∠CEO=45°，

∴FE=FC=2，

∴E（3，0），

∵C（1，2），

∴直线AE解析式为y=﹣x+3②，

联立①②解得x=2，y=1，

∴M（2，1）．

【解析】（1）由角平分线得出∠CAO=∠BAO，由平行线得出∠CAO=∠AOG，即∠BAO=∠AOG，即可；（2）先判断出点F是BC中点，再用中位线得出AG=BG，从而判断出△AOB是直角三角形，即可；（3）先求出OG，从而求出AC，得出点A，C坐标，最后求出直线OA，CM的解析式，即可求出它们的交点坐标．
【考点精析】利用角平分线的性质定理和等腰三角形的性质对题目进行判断即可得到答案，需要熟知定理1：在角的平分线上的点到这个角的两边的距离相等； 定理2：一个角的两边的距离相等的点，在这个角的平分线上；等腰三角形的两个底角相等（简称：等边对等角）．