题目内容
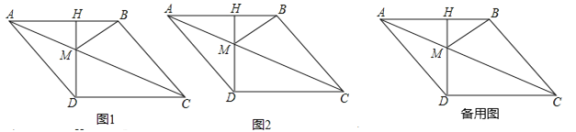
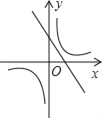
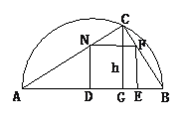
【题目】在直径为AB的半圆内，划出一块三角形区域，如图所示，使三角形的一边为AB，顶点C在半圆圆周上，其它两边分别为6和8，现要建造一个内接于△ABC的矩形水池DEFN，其中D、E在AB上，如图24-94的设计方案是使AC=8，BC=6．
（1）求△ABC的边AB上的高h．
（2）设DN=x，且
，当x取何值时，水池DEFN的面积最大？
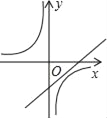
（3）实际施工时，发现在AB上距B点1．85的M处有一棵大树，问：这棵大树是否位于最大矩形水池的边上？如果在，为了保护大树，请设计出另外的方案，使内接于满足条件的三角形中欲建的最大矩形水池能避开大树．
【答案】（1）4.8 （2）2.4（3）见解析
【解析】试题分析：
首先利用勾股定理求得
的长．再利用三角形面积的两种求法解得高
的值．
（2）根据相似形对应边成比例列出矩形面积关于
的关系式S矩形DEFN
利用二次函数的性质求关系式的最大值．
（3）根据（2）知，知道的取值，此时S矩形DEFN最大，求得
的值．再利用勾股定理求得
的值，并与1.85比较大小．
试题解析：(1)过C作CG⊥AB于G，则CG=h，
在Rt△ABC中,
根据三角形面积公式得：
(2)∵如图,NF∥AB，
∴△CNF∽△CAB
∴
∴S矩形DEFN
则当x=2.4时,S矩形DEFN最大；
(3)当S矩形DEFN最大，x=2.4，
过点C作CG⊥AB于点G，
∵△ABC是直角三角形，AC=8，BC=6，
∴AB=10，
∵
∴F为BC中点，
在Rt△FEB中，EF=2.4，BF=3
∵BM=1.85
∴BM>EB
故文物必位于欲修建的建筑物边上，应重新设计方案
∵x=2.4时，NF=5
∴AD=3.2
由圆的对称性知：满足题设条件的设计方案是：
将最大面积的建筑物建在使AC=6，BC=8，且C点在半圆周上的△ABC中.
【题目】为了提高学生书写汉字的能力，增强保护汉字的意识，某市举办了首届“汉字听写大赛”，经选拔后有50名学生参加决赛，这50名学生同时听写50个汉字，若每正确听写出一个汉字得1分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如下：
组别 | 成绩x分 | 频数(人数) |
第1组 | 25≤x＜30 | 4 |
第2组 | 30≤x＜35 | 8 |
第3组 | 35≤x＜40 | 16 |
第4组 | 40≤x＜45 | a |
第5组 | 45≤x＜50 | 10 |
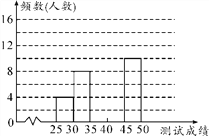
请结合图表完成下列各题：
(1)求表中a的值；
(2)请把频数分布直方图补充完整；
(3)若测试成绩不低于40分为优秀，则本次测试的优秀率是多少？
(4)第5组10名同学中，有4名男同学，现将这10名同学平均分成两组进行对抗练习，且4名男同学每组分两人，求小宇与小强两名男同学能分在同一组的概率．
