��Ŀ����
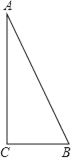
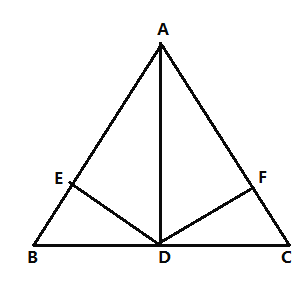
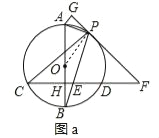
����Ŀ����ͼ��AB�ǡ�O��ֱ������CD��AB������ΪH��PΪ��AD��һ�㣬����PA��PB��PB��CD��E��
��1����ͼ��1������PC��CB����֤����BCP=��PED��
��2����ͼ��2������P����O�����߽�CD���ӳ����ڵ�E������A��PF�����ߣ�����ΪG����֤����APG=![]() ��F��
��F��
��3����ͼ��3����ͼ��2���������£�����PH����PH=PF��3PF=5PG��BE=2![]() �����O��ֱ��AB��
�����O��ֱ��AB��

���𰸡���1������������2������������3��AB=15
��������
��1���ɴ��������ó���CPB=��BCD�����ݡ�BCP=��BCD+��PCD=��CPB+��PCD=��PED���ɵ�֤��
��2������OP��֪OP=OB����֤��FPE=��FEP�á�F+2��FPE=180�㣬���ɡ�APG+��FPE=90��2��APG+2��FPE=180�㣬�ݴ˿ɵ�2��APG=��F���ݴ˼��ɵ�֤��
��3������AE��ȡAE�е�N������HN��PN������E��EM��PF����֤��PAE=��F����tan��PAE=tan��F��![]() ����֤��GAP=��MPE����sin��GAP=sin��MPE��
����֤��GAP=��MPE����sin��GAP=sin��MPE��![]() ���Ӷ��ó�
���Ӷ��ó�![]() ����MF=GP����3PF=5PG��
����MF=GP����3PF=5PG��![]() ������PG=3k����PF=5k��MF=PG=3k��PM=2k���ɡ�FPE=��PEF֪PF=EF=5k��EM=4k��PE=2
������PG=3k����PF=5k��MF=PG=3k��PM=2k���ɡ�FPE=��PEF֪PF=EF=5k��EM=4k��PE=2![]() k��AP=
k��AP=![]() k��֤��PEM=��ABP��BP=3
k��֤��PEM=��ABP��BP=3![]() k���̶��ɵ�BE=
k���̶��ɵ�BE=![]() k=2���ݴ����k=2���Ӷ��ó�AP��BP�ij������ù��ɶ����ɵô𰸣�
k=2���ݴ����k=2���Ӷ��ó�AP��BP�ij������ù��ɶ����ɵô𰸣�
֤������1����AB�ǡ�O��ֱ����AB��CD��
���CPB=��BCD��
���BCP=��BCD+��PCD=��CPB+��PCD=��PED��
���BCP=��PED��
��2������OP����OP=OB��
���OPB=��OBP��
��PF�ǡ�O�����ߣ�
��OP��PF�����OPF=90�㣬
��FPE=90�㩁��OPE��
�ߡ�PEF=��HEB=90�㩁��OBP��
���FPE=��FEP��
��AB�ǡ�O��ֱ����
���APB=90�㣬
���APG+��FPE=90�㣬
��2��APG+2��FPE=180�㣬
�ߡ�F+��FPE+��PEF=180�㣬
�ߡ�F+2��FPE=180��
��2��APG=��F��
���APG=![]() ��F��
��F��
��3������AE��ȡAE�е�N������HN��PN������E��EM��PF��M��
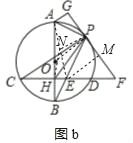
�ɣ�2��֪��APB=��AHE=90�㣬
��AN=EN��
��A��H��E��P�ĵ㹲Բ��
���PAE=��PHF��
��PH=PF��
���PHF=��F��
���PAE=��F��
tan��PAE=tan��F��
��![]() ��
��
�ɣ�2��֪��APB=��G=��PME=90�㣬
���GAP=��MPE��
��sin��GAP=sin��MPE��
��![]() ��
��
��![]() ��
��
��MF=GP��
��3PF=5PG��
��![]() ��
��
��PG=3k����PF=5k��MF=PG=3k��PM=2k
�ɣ�2��֪��FPE=��PEF��
��PF=EF=5k��
��EM=4k��
��tan��PEM=![]() ��tan��F=
��tan��F=![]() ��
��
��tan��PAE=![]() ��
��
��PE=![]() ��
��
��AP=![]() k��
k��
�ߡ�APG+��EPM=��EPM+��PEM=90�㣬
���APG=��PEM��
�ߡ�APG+��OPA=��ABP+��BAP=90�����ҡ�OAP=��OPA��
���APG=��ABP��
���PEM=��ABP��
��tan��ABP=tan��PEM����![]() ��
��
��![]() ��
��
��BP=3![]() k��
k��
��BE=![]() k=2
k=2![]() ��
��
��k=2��
��AP=3![]() ��BP=6
��BP=6![]() ��
��
���ݹ��ɶ����ã�AB=15��