题目内容
若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根,则有x1+x2=-| b |
| a |
| c |
| a |
(1)S1=
(2)当n为不小于3的整数时,由(1)猜想Sn,Sn-1,Sn-2有何关系?
(3)利用(2)中猜想求(
1+
| ||
| 2 |
1-
| ||
| 2 |
分析:(1)根据根与系数的关系,写出α+β,αβ的值,然后运用完全平方公式和立方和公式进行计算,求出S1,S2,S3,S4的值.
(2)利用(1)中S2=3,S3=4,S4=7,猜想Sn=Sn-1+Sn-2,然后由α,β是方程的根,得到α2=α+1,β,2=β+1进行证明.
(3)根据(2)中的猜想得到上式为S7=S6+S5进行计算求出式子的值.
(2)利用(1)中S2=3,S3=4,S4=7,猜想Sn=Sn-1+Sn-2,然后由α,β是方程的根,得到α2=α+1,β,2=β+1进行证明.
(3)根据(2)中的猜想得到上式为S7=S6+S5进行计算求出式子的值.
解答:解:(1)根据根与系数的关系有:
α+β=1,αβ=-1.
∴S1=α+β=1.
S2=α2+β2=(α+β)2-2αβ=1+2=3.
S3=α3+β3=(α+β)(α2-αβ+β2)=(α+β)2-3αβ=1+3=4.
S4=α4+β4=(α2+β2)2-2α2β2=9-2=7.
(2)由(1)得:Sn=Sn-1+Sn-2.
证明:∵α,β是方程的根,∴有:α2=α+1,β2=β+1,
Sn-1+Sn-2=αn-1+βn-1+αn-2+βn-2
=
+
+
+
=
+
=αn+βn=Sn.
故Sn=Sn-1+Sn-2.
(3)由(2)有:
(
)7+(
)7=S7=S6+S5
=S5+S4+S4+S3
=S4+S3+2S4+S3
=3S4+2S3
=3×7+2×4=29.
α+β=1,αβ=-1.
∴S1=α+β=1.
S2=α2+β2=(α+β)2-2αβ=1+2=3.
S3=α3+β3=(α+β)(α2-αβ+β2)=(α+β)2-3αβ=1+3=4.
S4=α4+β4=(α2+β2)2-2α2β2=9-2=7.
(2)由(1)得:Sn=Sn-1+Sn-2.
证明:∵α,β是方程的根,∴有:α2=α+1,β2=β+1,
Sn-1+Sn-2=αn-1+βn-1+αn-2+βn-2
=
| αn |
| α |
| αn |
| α2 |
| βn |
| β |
| βn |
| β2 |
=
| αn(1+α) |
| α2 |
| βn(1+β) |
| β2 |
=αn+βn=Sn.
故Sn=Sn-1+Sn-2.
(3)由(2)有:
(
1+
| ||
| 2 |
1-
| ||
| 2 |
=S5+S4+S4+S3
=S4+S3+2S4+S3
=3S4+2S3
=3×7+2×4=29.
点评:本题考查的是一元二次方程的根与系数的关系,(1)题根据根与系数的关系,运用乘法公式计算求出S1,S2,S3,S4的值.(2)题以(1)题结果为依据猜想Sn,Sn-1,Sn-2的关系,并根据α,β是方程的根进行证明.(3)题利用(2)题的结论进行计算求出式子的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•兰州)若x1、x2是关于一元二次方程ax2+bx+c(a≠0)的两个根,则方程的两个根x1、x2和系数a、b、c有如下关系:x1+x2=-
(2012•兰州)若x1、x2是关于一元二次方程ax2+bx+c(a≠0)的两个根,则方程的两个根x1、x2和系数a、b、c有如下关系:x1+x2=-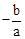 ,x1•x2=
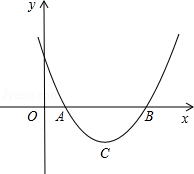
,x1•x2=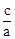 .把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B连个交点间的距离为:AB=|x1-x2|=
.把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B连个交点间的距离为:AB=|x1-x2|=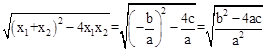
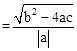 。
。