题目内容
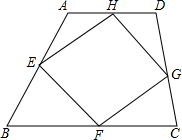 如图,已知四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点,
如图,已知四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点,①求证:四边形EFGH是平行四边形.
②探索下列问题,并选择一个进行证明.
a.原四边形ABCD的对角线AC、BD满足
AC⊥BD
AC⊥BD
时,四边形EFGH是矩形.b.原四边形ABCD的对角线AC、BD满足
AC=BD
AC=BD
时,四边形EFGH是菱形.c.原四边形ABCD的对角线AC、BD满足
AC⊥BD且AC=BD
AC⊥BD且AC=BD
时,四边形EFGH是正方形.分析:①首先连接AC,BD,由三角形中位线的性质,可判定EH∥FG,GH∥EF,继而可证得四边形EFGH是平行四边形.
②a、由①可得当原四边形ABCD的对角线AC、BD满足AC⊥BD时,四边形EFGH是矩形.
b、由①可得原四边形ABCD的对角线AC、BD满足AC=BD时,四边形EFGH是菱形.
c、由a与b可得:原四边形ABCD的对角线AC、BD满足AC⊥BD且AC=BD时,四边形EFGH是正方形.
②a、由①可得当原四边形ABCD的对角线AC、BD满足AC⊥BD时,四边形EFGH是矩形.
b、由①可得原四边形ABCD的对角线AC、BD满足AC=BD时,四边形EFGH是菱形.
c、由a与b可得:原四边形ABCD的对角线AC、BD满足AC⊥BD且AC=BD时,四边形EFGH是正方形.
解答: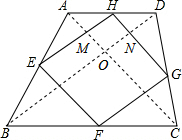 解:①连接AC,BD,
解:①连接AC,BD,
∵四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点,
∴EH∥BD,FG∥BD,
∴EH∥FG,
同理:GH∥EF,
∴四边形EFGH是平行四边形.
②a、当AC⊥BD时,四边形EFGH是矩形.
∵由①得:四边形MONH是平行四边形,
∴当AC⊥BD时,四边形MONH是矩形,
∴∠EHG=90°,
∴四边形EFGH是矩形.
b、当AC=BD时,四边形EFGH是菱形.
∵HG=
AC,EH=
BD,
∴EH=GH,
∴四边形EFGH是菱形;
c、由a与b可得:原四边形ABCD的对角线AC、BD满足AC⊥BD且AC=BD时,四边形EFGH是正方形.
故答案为:a、AC⊥BD,b、AC=BD,c、AC⊥BD且AC=BD.
 解:①连接AC,BD,
解:①连接AC,BD,∵四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点,
∴EH∥BD,FG∥BD,
∴EH∥FG,
同理:GH∥EF,
∴四边形EFGH是平行四边形.
②a、当AC⊥BD时,四边形EFGH是矩形.
∵由①得:四边形MONH是平行四边形,
∴当AC⊥BD时,四边形MONH是矩形,
∴∠EHG=90°,
∴四边形EFGH是矩形.
b、当AC=BD时,四边形EFGH是菱形.
∵HG=
| 1 |
| 2 |
| 1 |
| 2 |
∴EH=GH,
∴四边形EFGH是菱形;
c、由a与b可得:原四边形ABCD的对角线AC、BD满足AC⊥BD且AC=BD时,四边形EFGH是正方形.
故答案为:a、AC⊥BD,b、AC=BD,c、AC⊥BD且AC=BD.
点评:此题考查了中点四边形的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
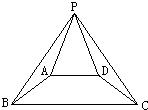 15、如图,已知四边形ABCD是等腰梯形,AB=DC,AD∥BC,PB=PC.求证:PA=PD.
15、如图,已知四边形ABCD是等腰梯形,AB=DC,AD∥BC,PB=PC.求证:PA=PD.
 的延长线分别交于点F、E,且
的延长线分别交于点F、E,且 (2013•梧州)如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
(2013•梧州)如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.