��Ŀ����
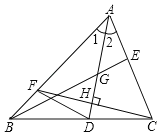
����Ŀ����ͼ��ʾ���ڡ�ABC�У�AD�ǡ�BAC��ƽ���ߣ�G��AD��һ�㣬��AG��DG������BG���ӳ�BG��AC��E���ֹ�C��AD�Ĵ��߽�AD��H����ABΪF��������˵����ȷ����_____������ţ���
��D��BC���е㣻����CDA����2����BE�ǡ�ABC�ı�AC�ϵ����ߣ�
��CHΪ��ACD�ı�AD�ϵĸߣ�����AFCΪ���������Σ�
������DF����CF��6��AD��8�����ı���ACDF�����Ϊ24��
���𰸡��ڢܢݢޣ�
��������
���ݵ��������εĶ��塢�����ε����ߡ������εĸߵĸ�������жϣ��Խ��ߴ�ֱ���ı��ε�������Խ��߳˻���һ�룻
�⣺�ٴ�������۳���������ABC�ǵ��������Σ���Ȼ�����ܣ��ʢٴ���
����ȷ���ߡ�ADC����1+��ABD����1����2��
���ADC����2���ʢ���ȷ��
�۴�������۳��������AG��GD��AE��EC��
��EG��BC����Ȼ�����ܣ��ʢ۴���
����ȷ����CH��AD��
��CHΪ��ACD�ı�AD�ϵĸߣ��ʢ���ȷ��
����ȷ���ߡ�1����2��AD��AD����AHF����AHC��90����
���AHF�ա�AHC��ASA����
��AF��AC���ʢ���ȷ��
����ȷ����AD��CF��
��S�ı���ACDF��![]() ��AD��CF��
��AD��CF��![]() ��6��8��24��
��6��8��24��
�ʴ�Ϊ�ڢܢݢޣ�

 �Űٷֿ�ʱ����ϵ�д�
�Űٷֿ�ʱ����ϵ�д�