题目内容
(本小题满分14分)平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别为(0,3)、( ,0),将此平行四边形绕点0顺时针旋转90°,得到平行四边形
,0),将此平行四边形绕点0顺时针旋转90°,得到平行四边形 。
。
(1)若抛物线过点C,A, ,求此抛物线的解析式;
,求此抛物线的解析式;
(2)求平行四边形ABOC和平行四边形 重叠部分△
重叠部分△ 的周长;
的周长;
(3)点M是第一象限内抛物线上的一动点,间:点M在何处时△ 的面积最大?最大面积是多少?并求出此时点M的坐标。
的面积最大?最大面积是多少?并求出此时点M的坐标。
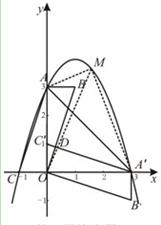
解:(1)∵ 由
由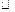 ABOC旋转得到,且点A的坐标为(0,3),
ABOC旋转得到,且点A的坐标为(0,3),
点 的坐标为(3,0)。
的坐标为(3,0)。
所以抛物线过点C(-1,0),A(0,3), (3,0)设抛物线的解析式为
(3,0)设抛物线的解析式为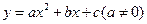 ,可得
,可得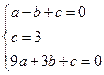 解得
解得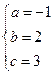
∴过点C,A, 的抛物线的解析式为
的抛物线的解析式为 。
。
(2)因为AB∥CO,所以∠OAB=∠AOC=90°。
∴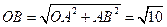 ,又
,又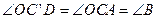 .
.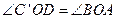 ,∴
,∴ 又
又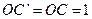 ,
,
∴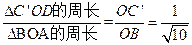 ,又△ABO的周长为
,又△ABO的周长为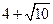 。
。
∴ 的周长为
的周长为 。
。
(3)连接OM,设M点的坐标为 ,
,
∵点M在抛物线上,∴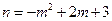 。
。
∴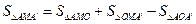
=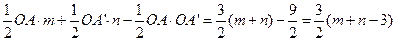
=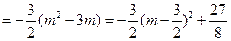
因为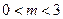 ,所以当
,所以当 时,
时,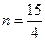 。△AMA’的面积有最大值
。△AMA’的面积有最大值
所以当点M的坐标为(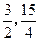 )时,△AMA’的面积有最大值,且最大值为
)时,△AMA’的面积有最大值,且最大值为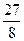 。
。
解析

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
 如图13,二次函数
如图13,二次函数 与y轴交于点C(0,
与y轴交于点C(0, ), 与x轴交于点A、 B,点A的坐标为(2,0).
), 与x轴交于点A、 B,点A的坐标为(2,0).
 与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为(
与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为( ,0).问:是否存在这样的直线
,0).问:是否存在这样的直线 与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线
与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线 与抛物线交于点B、C.
与抛物线交于点B、C.
 与
与 的面积。
的面积。 时,
时, 是以BC为斜边的直角三角形,若存在,求出b;若不存在,说明理由.
是以BC为斜边的直角三角形,若存在,求出b;若不存在,说明理由.