题目内容
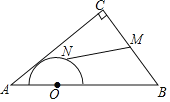
【题目】如图,在由边长都为1的小正方形组成的网格中,点![]() ,
,![]() ,
,![]() 均为格点,点
均为格点,点![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 上的动点,且满足
上的动点,且满足![]() .
.
(1)线段![]() 的长度等于__________;
的长度等于__________;
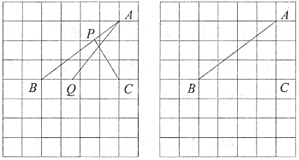
(2)当线段![]() 取得最小值时,请借助无刻度直尺在给定的网格中画出线段
取得最小值时,请借助无刻度直尺在给定的网格中画出线段![]() 和
和![]() ,并简要说明你是怎么画出点Q,P的:_______________________.
,并简要说明你是怎么画出点Q,P的:_______________________.
【答案】5 取格点![]() .连接
.连接![]() ,它们相交于点
,它们相交于点![]() ,连接
,连接![]() ,分别交
,分别交![]() 于点
于点![]() ,则线段
,则线段![]() 和
和![]() 即为所求.
即为所求.
【解析】
(1)利用勾股定理求出AB的长即可;(2)要使AQ+PC有最小值,则应把AQ与PC转换到一条直线,利用全等三角形可确定∠QBT的位置,连接EF,利用相似三角形可确定T点位置,连接AT交BC于Q,则QT=PC,根据全等三角形确定∠ACP,据此即可得出点P、Q的位置.
(1)AB=![]() =5.
=5.
(2)∵要使AQ+PC有最小值,
∴应把AQ与PC转换到一条直线,即使QT=PC,得AQ+PC=AT,
∴作△BQT≌△APC即可,
∴应作∠CBT=∠BAC,BT=AC=3,
∴连接BD,则∠CBT=∠BAC,
∵BD=5,
∴要使BT=3,则![]() =
=![]() ,
,
∴连接EF,则![]() =
=![]() =
=![]() ,即BT=3,
,即BT=3,
∴连接AT,交BC于Q,则Q点即为所求,
∵△BQT≌△APC,
∴∠BTA=∠ACP,
∴只要作△ABT的全等三角形即可,
∵AC=BT,∠ABT=90°,AB=5,
∴作GA⊥AC,AG=5,则△ABT≌△GAC,
∴连接CG,交AB于P,则∠ACP=∠ATB,则P点即为所求.

故答案为:5;取格点![]() .连接
.连接![]() ,它们相交于点
,它们相交于点![]() ,连接
,连接![]() ,分别交
,分别交![]() 于点
于点![]() ,则线段
,则线段![]() 和
和![]() 即为所求.
即为所求.

【题目】某单位要印刷“市民文明出行,遵守交通安全”的宣传材料.甲印刷厂提出:每份材料收1元印刷费,另收150元的制版费;乙印刷厂提出:每份材料收2.5元印刷费,不收制版费.设在同一家印刷厂一次印制数量为![]() 份(
份(![]() 为正整数).
为正整数).
(1)根据题意,填写下表:
一次印制数量(份) | 5 | 10 | 20 | … |
|
甲印刷厂收费(元) | 155 | … | |||
乙印刷厂收费(元) | 12.5 | … |
(2)在印刷品数量大于800份的情况下选哪家印刷厂印制省钱?