Question

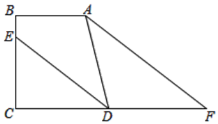
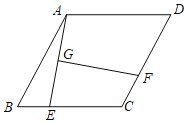
【题目】如图，四边形ABCD为菱形，∠D=60°，AB=4，E为边BC上的动点，连接AE，作AE的垂直平分线GF交直线CD于F点，垂足为点G，则线段GF的最小值为____________．

Answer 1

【答案】3

【解析】

作辅助线，构建三角形全等，证明Rt△AFM≌Rt△EFN（HL），得∠AFM=∠EFN，再证明△AEF是等边三角形，计算FG=AG=AE，确认当AE⊥BC时，即AE=2时，FG最小．

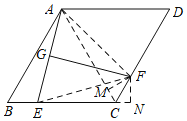
解：连接AC，过点F作FM⊥AC于，作FN⊥BC于N，连接AF、EF，

∵四边形ABCD是菱形，且∠D=60°，

∴∠B=∠D=60°，AD∥BC，

∴∠FCN=∠D=60°=∠FCM，

∴FM=FN，

∵FG垂直平分AE，

∴AF=EF，

∴Rt△AFM≌Rt△EFN（HL），

∴∠AFM=∠EFN，

∴∠AFE=∠MFN，

∵∠FMC=∠FNC=90°，∠MCN=120°，

∴∠MFN=60°，

∴∠AFE=60°，

∴△AEF是等边三角形，

∴FG=AG=AE，

∴当AE⊥BC时，Rt△ABE中，∠B=60°，

∴∠BAE=30°，

∵AB=4，

∴BE=2，AE=2，

∴当AE⊥BC时，即AE=2时，FG最小，最小为3；

故答案为：3．