题目内容
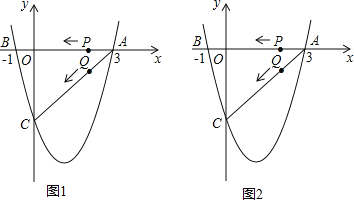
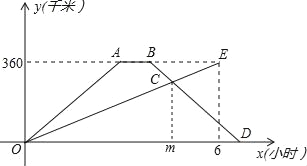
【题目】(8分)快、慢两车分别从相距360千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,快车到达乙地后,停留1小时,然后按原路原速返回,快车比慢车晚1小时到达甲地,快、慢两车距各自出发地的路程y(千米)与出发后所用的时间x(小时)的关系如图.
请结合图象信息解答下列问题:
(1)慢车的速度是 千米/小时,快车的速度是 千米/小时;
(2)求m的值,并指出点C的实际意义是什么?
(3)在快车按原路原速返回的过程中,快、慢两车相距的路程为150千米时,慢车行驶了多少小时?
【答案】(1)60,120;(2)C点表示![]() 小时时,慢车在距离乙地280千米处,快车在距离甲地280千米处;慢车行驶了5.5小时.
小时时,慢车在距离乙地280千米处,快车在距离甲地280千米处;慢车行驶了5.5小时.
【解析】试题分析:(1)根据速度=路程÷时间求出慢车的速度,再求出快车到达甲地的时间,然后根据速度=路程÷时间列式计算即可求出快车的速度;
(2)根据两车距离出发地的路程列出方程,然后求出m的值,再求出y值,然后说出两车的位置即可;
(3)利用两车与甲地的距离表示出两车间的距离,然后求解即可.
试题解析:(1)慢车速度=![]() =60千米/小时,
=60千米/小时,
∵快车到达乙地后,停留1小时,快车比慢车晚1小时到达甲地,
∴快车返回甲地的时间为6+1﹣1=6,
∴快车速度=![]() =120千米/小时;
=120千米/小时;
故答案为:60,120;
(2)由题意得,60m=360×2﹣120(m﹣1),
解得m=![]() ,
,
60×![]() =280km,
=280km,
所以,C点表示![]() 小时时,慢车在距离乙地280千米处,快车在距离甲地280千米处;
小时时,慢车在距离乙地280千米处,快车在距离甲地280千米处;
(3)设慢车行驶了x小时,
由题意得,60x﹣120(x﹣![]() ﹣1)=150,
﹣1)=150,
解得x=5.5小时,
答:慢车行驶了5.5小时.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目