题目内容
已知:在Rt△ABC中,AB=BC,在Rt△ADE中,AD=DE,连接EC,取EC的中点M,连接DM和BM.(1)若点D在边AC上,点E在边AB上且与点B不重合,如图1,探索BM、DM的关系并给予证明;
(2)如果将图1中的△ADE绕点A逆时针旋转小于45°的角,如图2,那么(1)中的结论是否仍成立?如果不
 成立,请举出反例;如果成立,请给予证明.
成立,请举出反例;如果成立,请给予证明.
分析:(1)要求BM和DM的关系,可从角的度数入手,由题意,BM是直角三角形CBE斜边上的中线,因此BM=CM,∠MCB=∠MBC,
∠BME=2∠MCB,同理可得出∠DME=2∠DCM,根据三角形ABC是个等腰直角三角形,那么∠DCM+∠BCE=45°,因此∠BME+∠DME=2(∠DCM+∠BCM)=90°,由此我们可得出∠BMD=90°,那么BM和DM是互相垂直的;
(2)可通过构建三角形来求解,连接CD和EF,连接BD,延长DM至点F,使得DM=MF,连接BF、FC,延长ED交AC于点H.那么我们只要证明三角形DBF是个等腰三角形就可以了(等腰三角形三线合一).那么关键就是证明三角形ADB和CFB全等.这两个三角形中已知的只有AB=BC,根据EM=MC,DM=MF,那么四边形DEFC就是平行四边形,ED=CF=AD,那么只要得出这两组对应边的夹角相等即可得出全等的结论,我们发现∠BCF=∠ACF-45°,∠ACF=∠AHE,那么只要证得∠BAD=∠AHE-45°即可,∠BAD=45°-∠DAH=45°-(90°-∠AHE)=∠AHE-45°,由此可得出∠BAD=∠BCF,那么就能证得两三角形全等了(SAS).那么就能证得DBF是个等腰三角形了根据等腰三角形三线合一的特点,也就能得出BM⊥DM了.
∠BME=2∠MCB,同理可得出∠DME=2∠DCM,根据三角形ABC是个等腰直角三角形,那么∠DCM+∠BCE=45°,因此∠BME+∠DME=2(∠DCM+∠BCM)=90°,由此我们可得出∠BMD=90°,那么BM和DM是互相垂直的;
(2)可通过构建三角形来求解,连接CD和EF,连接BD,延长DM至点F,使得DM=MF,连接BF、FC,延长ED交AC于点H.那么我们只要证明三角形DBF是个等腰三角形就可以了(等腰三角形三线合一).那么关键就是证明三角形ADB和CFB全等.这两个三角形中已知的只有AB=BC,根据EM=MC,DM=MF,那么四边形DEFC就是平行四边形,ED=CF=AD,那么只要得出这两组对应边的夹角相等即可得出全等的结论,我们发现∠BCF=∠ACF-45°,∠ACF=∠AHE,那么只要证得∠BAD=∠AHE-45°即可,∠BAD=45°-∠DAH=45°-(90°-∠AHE)=∠AHE-45°,由此可得出∠BAD=∠BCF,那么就能证得两三角形全等了(SAS).那么就能证得DBF是个等腰三角形了根据等腰三角形三线合一的特点,也就能得出BM⊥DM了.
解答: 解:(1)BM=DM,BM⊥DM,
解:(1)BM=DM,BM⊥DM,
在Rt△EBC中,M是斜边EC的中点,
∴BM=
EC=EM=MC,
∴∠EMB=2∠ECB.
在Rt△EDC中,M是斜边EC的中点,
∴DM=
EC=EM=MC.
∴∠EMD=2∠ECD.
∴BM=DM,∠EMD+∠EMB=2(∠ECD+∠ECB),
∵∠ECD+∠ECB=∠ACB=45°,
∴∠BMD=2∠ACB=90°,即BM⊥DM.
(2):(1)中的结论仍成立,
连接CD和EF,连接BD,延长DM至点F,使得DM=MF,连接BF、FC,延长ED交AC于点H.
∵DM=MF,EM=MC,
∴四边形CDEF是平行四边形,
∴DE∥CF,ED=CF,
∵ED=AD,
∴AD=CF.
∵DE∥CF,
∴∠AHE=∠ACF.
∵∠BAD=45°-∠DAH=45°-(90°-∠AHE)=∠AHE-45°,∠BCF=∠ACF-45°,
∴∠BAD=∠BCF.
又∵AB=BC,
∴△ABD≌△CBF,
∴BD=BF,∠ABD=∠CBF,
∵∠ABD+∠DBC=∠CBF+∠DBC,
∴∠DBF=∠ABC=90°.
在Rt△DBF中,由BD=BF,DM=MF,得BM=DM且BM⊥DM.
 解:(1)BM=DM,BM⊥DM,
解:(1)BM=DM,BM⊥DM,在Rt△EBC中,M是斜边EC的中点,
∴BM=
| 1 |
| 2 |
∴∠EMB=2∠ECB.
在Rt△EDC中,M是斜边EC的中点,
∴DM=
| 1 |
| 2 |
∴∠EMD=2∠ECD.
∴BM=DM,∠EMD+∠EMB=2(∠ECD+∠ECB),
∵∠ECD+∠ECB=∠ACB=45°,
∴∠BMD=2∠ACB=90°,即BM⊥DM.
(2):(1)中的结论仍成立,
连接CD和EF,连接BD,延长DM至点F,使得DM=MF,连接BF、FC,延长ED交AC于点H.
∵DM=MF,EM=MC,
∴四边形CDEF是平行四边形,
∴DE∥CF,ED=CF,
∵ED=AD,
∴AD=CF.
∵DE∥CF,
∴∠AHE=∠ACF.
∵∠BAD=45°-∠DAH=45°-(90°-∠AHE)=∠AHE-45°,∠BCF=∠ACF-45°,
∴∠BAD=∠BCF.
又∵AB=BC,
∴△ABD≌△CBF,
∴BD=BF,∠ABD=∠CBF,
∵∠ABD+∠DBC=∠CBF+∠DBC,
∴∠DBF=∠ABC=90°.
在Rt△DBF中,由BD=BF,DM=MF,得BM=DM且BM⊥DM.
点评:本题解题的关键是通过构建全等三角形来得出线段相等,然后根据线段相等得出所求的结论.

练习册系列答案
相关题目
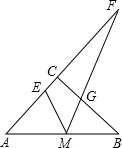 如图,已知:在Rt△ABC中,∠ACB=90°,AC=BC=4,M是边AB的中点,E、G分别是边AC、BC上的一点,∠EMG=45°,AC与MG的延长线相交于点F.
如图,已知:在Rt△ABC中,∠ACB=90°,AC=BC=4,M是边AB的中点,E、G分别是边AC、BC上的一点,∠EMG=45°,AC与MG的延长线相交于点F.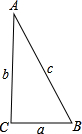 已知:在Rt△ABC中,∠C=90°,∠A=30°,b=
已知:在Rt△ABC中,∠C=90°,∠A=30°,b=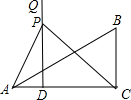 重合),过D作DQ⊥AC(DQ与AB在AC的同侧);点P从D点出发,在射线DQ上运动,连接PA、PC.
重合),过D作DQ⊥AC(DQ与AB在AC的同侧);点P从D点出发,在射线DQ上运动,连接PA、PC.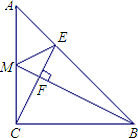 已知:在Rt△ABC中,∠C=90°,AC=BC,M是AC的中点,连接BM,CF⊥MB,F是垂足,延长CF交AB于点E.求证:∠AME=∠CMB.
已知:在Rt△ABC中,∠C=90°,AC=BC,M是AC的中点,连接BM,CF⊥MB,F是垂足,延长CF交AB于点E.求证:∠AME=∠CMB. 已知:在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.
已知:在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.