Question

【题目】已知，在△ABC中，∠ACB＝30°

（1）如图1，当AB＝AC＝2，求BC的值；

（2）如图2，当AB＝AC，点P是△ABC内一点，且PA＝2，PB＝，PC＝3，求∠APC的度数；

（3）如图3，当AC＝4，AB＝（CB＞CA），点P是△ABC内一动点，则PA+PB+PC的最小值为　 　．

Answer 1

【答案】（1）BC＝2；（2）∠APC＝120°；（3）．

【解析】

作AP⊥BC于P，因为AC＝2，∠C＝30°，利用求得PC，再利用垂径定理得BP=PC，即可求解.

因为AB＝AC，∠C＝30°，所以∠BAC＝120°，将△APB绕点A逆时针旋转120°得到△QAC，所以，因为∠PAQ＝120°，所以PQ＝2 ，PQ2+PC2＝QC2，∠QPC＝90°，APQ＝30°，∠APC＝∠APQ +∠QPC代入即可求解.

将△BCP绕点C逆时针旋转60°得到△CB′P′，连接PP′，AB′，则∠ACB′＝90°，因为PA+PB+PC＝PA+PP′+P′B′，所以当A，P，P′，B′共线时，PA+PB+PC的值最小，最小值＝AB′的长，再根据勾股定理即可求解.

解：（1）如图1中，作AP⊥BC于P．

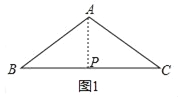
∵AB＝AC，AP⊥BC，

∴BP＝PC，

在Rt△ACP中，∵AC＝2，∠C＝30°，

∴PC＝ACcos30°＝，

∴BC＝2PC＝2．

（2）如图2中，

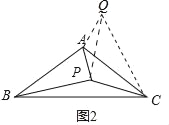
∵AB＝AC，∠C＝30°，

∴∠BAC＝120°，

将△APB绕点A逆时针旋转120°得到△QAC．

∴PA＝AQ＝2，PB＝QC＝，

∵∠PAQ＝120°，

∴PQ＝2，

∴PQ2+PC2＝QC2，

∴∠QPC＝90°，

∵∠APQ＝30°，

∴∠APC＝30°+90°＝120°．

（3）如图3中，将△BCP绕点C逆时针旋转60°得到△CB′P′，连接PP′，AB′，则∠ACB′＝90°．

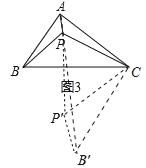
∵PA+PB+PC＝PA+PP′+P′B′，

∴当A，P，P′，B′共线时，PA+PB+PC的值最小最小值＝AB′的长，

p>由AB＝，AC＝4，∠C＝30°，可得BC＝CB′＝3，

∴AB′＝＝．

故答案为．