题目内容
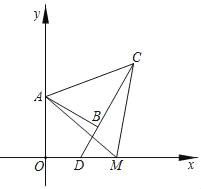
【题目】如图，在平面直角坐标系中，已知A（0，2），M（m，0）且m＞0，分别以AO、AM为边在∠AOM内部作等边△AOB和等边△AMC，连接CB并延长交x轴于点D，则C点的横坐标的值为（ ）
A. 
m+
B. m+
C. m+
D. m+
【答案】D
【解析】
根据等边三角形的性质可以得出OA=AB，AM=AC，由等式的性质就可以得出∠OAM=∠CAB，再利用△AOM≌△ABC，可得BC=OM=m，然后根据C点横坐标为
，
就可以得出结论.
∵△AOB、△AMC为等边三角形
∴∠OAB=∠MAC，OA=AB，AM=AC
∵∠OAB-∠MAB=∠OAM
∠MAC-∠MAB=∠CAB
∴∠OAM=∠CAB
∵
∴△AOM≌△ABC(SAS)
∴BC=OM=m，∠AOM=∠ABC=90.
∵∠BOM=90°-∠AOB=30°
∴∠ABD=90°，
∴∠AOM=∠ABD
∴∠AOM∠ABO=∠ABD∠AOB，
∴∠OBD=∠BOD=30°，
∴OD=OB.
∴∠CDM=∠OBD+∠BOD=60°
则C点横坐标为
=
m+
.
故答案为：D.
练习册系列答案
相关题目
