题目内容
已知a,b是整数,a≠b且-4≤a≤5,-4≤b≤5,则二次函数y=x2-(a+b)x+ab的最小值的最大值为 .
【答案】分析:首先求二次函数的最小值,然后再由a,b的范围求其最大值即可.
解答:解:由题意可得:
y=x2-(a+b)x+ab
=(x- )2-
)2- ,
,
当x= 时,y有最小值-
时,y有最小值-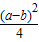 ,
,
∵a,b是整数,a≠b且-4≤a≤5,-4≤b≤5,
∴当(a-b)2=1时,- 有最大值,且最大值为
有最大值,且最大值为 ;
;
点评:本题考查二次函数最值,是基础题型.
解答:解:由题意可得:
y=x2-(a+b)x+ab
=(x-
 )2-
)2- ,
,当x=
 时,y有最小值-
时,y有最小值-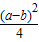 ,
,∵a,b是整数,a≠b且-4≤a≤5,-4≤b≤5,
∴当(a-b)2=1时,-
 有最大值,且最大值为
有最大值,且最大值为 ;
;点评:本题考查二次函数最值,是基础题型.

练习册系列答案
相关题目