题目内容
【题目】(8分)【问题情境】
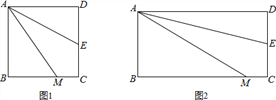
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
【探究展示】(1)证明:AM=AD+MC;
【拓展延伸】(2)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)中的结论是否成立?请作出判断,不需要证明.
【答案】(1)见解析;(2)仍然成立.
【解析】整体分析:
(1)延长AE、BC交于点N,由△ADE≌△NCE,证AD=NC,由角平分线,平行线得MA=MN;(2)与(1)的方法类似.
(1)证明:延长AE、BC交于点N,如图1,
∵四边形ABCD是正方形,∴AD∥BC.∴∠DAE=∠ENC.∵AE平分∠DAM,∴∠DAE=∠MAE.
∴∠ENC=∠MAE.∴MA=MN.
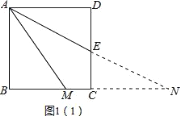
∴△ADE≌△NCE(AAS)
∴AD=NC.∴MA=MN=NC+MC=AD+MC.
(2)①结论AM=AD+MC仍然成立.
证明:延长AE、BC交于点P,如图2,
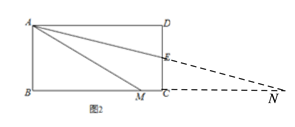
∵四边形ABCD是矩形,∴AD∥BC.∴∠DAE=∠EPC.
∵AE平分∠DAM,∴∠DAE=∠MAE.
∴∠EPC=∠MAE.∴MA=MP.
∴△ADE≌△PCE(AAS).
∴AD=PC.∴MA=MP=PC+MC=AD+MC.

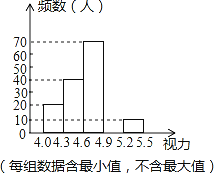
【题目】某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |
(1)在频数分布表中,a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,求视力正常的人数占被调查人数的百分比是多少?
【题目】某公司招聘职员,对甲、乙两位候选人进行了面试和笔试,面试中包括形体和口才,笔试中包括专业水平和创新能力考察,他们的成绩(百分制)如下表:
候选人 | 面试 | 笔试 | ||
形体 | 口才 | 专业水平 | 创新能力 | |
甲 | 86 | 90 | 96 | 92 |
乙 | 92 | 88 | 95 | 93 |
若公司根据经营性质和岗位要求认为:形体、口才、专业水平、创新能力按照5:5:4:6的比确定,请计算甲、乙两人各自的平均成绩,看看谁将被录取?