题目内容
【题目】如图,在直角坐标平面中,O为原点,点A的坐标为(20,0),点B在第一象限内,BO=10,sin∠BOA= ![]() .
. 
(1)在图中,求作△ABO的外接圆(尺规作图,不写作法但需保留作图痕迹);
(2)求点B的坐标与cos∠BAO的值;
(3)若A,O位置不变,将点B沿x轴向右平移使得△ABO为等腰三角形,请求出平移后点B的坐标.
【答案】
(1)解:如图所示:
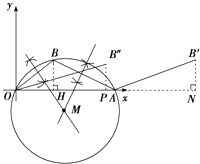
(2)解:如图,作BH⊥OA,垂足为H,
在Rt△OHB中,∵BO=10,sin∠BOA= ![]() ,
,
∴BH=6,
∴OH=8,∴点B的坐标为(8,6),
∵OA=20,OH=8,∴AH=12,
在Rt△AHB中,∵BH=6,
∴AB= ![]() =6
=6 ![]()
∴cos∠BAO= ![]()
(3)解:①当BO=AB时,∵AO=20,∴OH=10,
∴点B沿x轴正半轴方向平移2个单位,
②当AO=AB′时,∵AO=20,∴AB′=20,
过B′作B′N⊥x轴,
∵点B的坐标为(8,6),
∴B′N=6,∴AN= ![]() =2
=2 ![]() .
.
∴点B沿x轴正半轴方向平移(2 ![]() +12)个单位,
+12)个单位,
③当AO=OB″时,
∵AO=20,
∴OB″=20,
过B″作B″P⊥x轴.
∵B的坐标为(8,6),
∴B″P=6,
∴OP= ![]() =2
=2 ![]() ,
,
∴点B沿x轴正半轴方向平移(2 ![]() ﹣8)个单位,
﹣8)个单位,
综上所述当点B沿x轴正半轴方向平移2个单位、(2 ![]() +12)个单位,或(2
+12)个单位,或(2 ![]() ﹣8)个单位时,△ABO为等腰三角形
﹣8)个单位时,△ABO为等腰三角形
【解析】(1)作OB,AB的垂直平分线交于一点M,以点M为圆心,MA为半径画圆,则圆M即为所求;(2)如图,作BH⊥OA,垂足为H,在Rt△OHB中,由BO=10,sin∠BOA= ![]() ,得到BH=6,OH=8,求出点B的坐标为(8,6),根据OA=20,OH=8,求出AH=12,在Rt△AHB中,由BH=6,得到AB=
,得到BH=6,OH=8,求出点B的坐标为(8,6),根据OA=20,OH=8,求出AH=12,在Rt△AHB中,由BH=6,得到AB= ![]() =6
=6 ![]() ,求出cos∠BAO=
,求出cos∠BAO= ![]() ;(3)①当BO=AB时,由AO=20,得到OH=10,点B沿x轴正半轴方向平移2个单位;②当AO=AB′时,由AO=20,得到AB′=20,过B′作B′N⊥x轴,由点B的坐标为(8,6),得到B′N=6,AN=
;(3)①当BO=AB时,由AO=20,得到OH=10,点B沿x轴正半轴方向平移2个单位;②当AO=AB′时,由AO=20,得到AB′=20,过B′作B′N⊥x轴,由点B的坐标为(8,6),得到B′N=6,AN= ![]() =2
=2 ![]() .求得点B沿x轴正半轴方向平移(2
.求得点B沿x轴正半轴方向平移(2 ![]() +12)个单位,③当AO=OB″时,由AO=20,得到OB″=20,过B″作B″P⊥x轴.由B的坐标为(8,6),得到B″P=6,OP=
+12)个单位,③当AO=OB″时,由AO=20,得到OB″=20,过B″作B″P⊥x轴.由B的坐标为(8,6),得到B″P=6,OP= ![]() =2
=2 ![]() ,点B沿x轴正半轴方向平移(2
,点B沿x轴正半轴方向平移(2 ![]() ﹣8)个单位.
﹣8)个单位.

 字词句段篇系列答案
字词句段篇系列答案