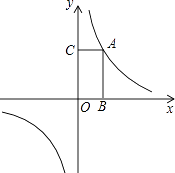题目内容
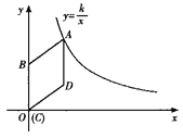
【题目】如图,已知直线y=![]() x与反比例函数y=
x与反比例函数y=![]() (k>0)的图象交于A,B两点,且点A的横坐标为4.
(k>0)的图象交于A,B两点,且点A的横坐标为4.
(1)求k的值.
(2)若反比例函数y=![]() 的图象上一点C的纵坐标为8,求△AOC的面积.
的图象上一点C的纵坐标为8,求△AOC的面积.
(3)若过原点O的另一条直线l交反比例函数y=![]() (k>0)的图象于P,Q两点(点P在第一象限),以A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.
(k>0)的图象于P,Q两点(点P在第一象限),以A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.

【答案】(1)8(2)15(3) (2,4)或(8,1)
【解析】(1)先根据直线的解析式求出A点的坐标,然后将A点坐标代入双曲线的解析式中即可求出k的值;
(2)由(1)得出的双曲线的解析式,可求出C点的坐标,由于△AOC的面积无法直接求出,因此可通过作辅助线,通过其他图形面积的和差关系来求得.(解法不唯一);
(3)由于双曲线是关于原点的中心对称图形,因此以A、B、P、Q为顶点的四边形应该是平行四边形,那么△POA的面积就应该是四边形面积的四分之一即6.可根据双曲线的解析式设出P点的坐标,然后参照(2)的三角形面积的求法表示出△POA的面积,由于△POA的面积为6,由此可得出关于P点横坐标的方程,即可求出P点的坐标.
(1)∵点A横坐标为4,
把x=4代入y=![]() x中
x中
得y=2,
∴A(4,2),
∵点A是直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0)的交点,
(k>0)的交点,
∴k=4×2=8;
(2)如图,

∵点C在双曲线上,
当y=8时,x=1,
∴点C的坐标为(1,8).
过点A、C分别做x轴、y轴的垂线,垂足为M、N,得矩形DMON.
∵S矩形ONDM=32,S△ONC=4,S△CDA=9,S△OAM=4.
∴S△AOC=S矩形ONDM-S△ONC-S△CDA-S△OAM=32-4-9-4=15;
(3)∵反比例函数图象是关于原点O的中心对称图形,
∴OP=OQ,OA=OB,
∴四边形APBQ是平行四边形,
∴S△POA=S平行四边形APBQ×![]() =
=![]() ×24=6,
×24=6,
设点P的横坐标为m(m>0且m≠4),
得P(m,![]() ),
),
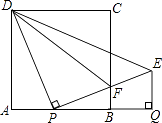
过点P、A分别做x轴的垂线,垂足为E、F,
∵点P、A在双曲线上,
∴S△POE=S△AOF=4,
若0<m<4,如图,

∵S△POE+S梯形PEFA=S△POA+S△AOF,
∴S梯形PEFA=S△POA=6.
∴![]() (2+
(2+![]() )(4-m)=6.
)(4-m)=6.
∴m1=2,m2=-8(舍去),
∴P(2,4);
若m>4,如图,

∵S△AOF+S梯形AFEP=S△AOP+S△
∴S梯形PEFA=S△POA=6.
∴![]() (2+
(2+![]() )(m-4)=6,
)(m-4)=6,
解得m1=8,m2=-2(舍去),
∴P(8,1).
∴点P的坐标是P(2,4)或P(8,1).