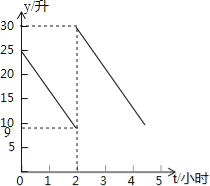МвДҝДЪИЭ
ЎҫМвДҝЎҝФД¶БАнҪв
ФЪЎчABCЦРЈ¬ABЎўBCЎўACИэұЯөДіӨ·ЦұрОӘ![]() Ўў
Ўў![]() Ўў2Ј¬ЗуХвёцИэҪЗРОөДГж»эЈ®
Ўў2Ј¬ЗуХвёцИэҪЗРОөДГж»эЈ®
Ҫв·ЁТ»ЈәИзНј1Ј¬ТтОӘЎчABCКЗөИСьИэҪЗРОЈ¬ІўЗТөЧACЈҪ2Ј¬ёщҫЭ№ҙ№Й¶ЁАнҝЙТФЗуөГөЧұЯөДёЯAFОӘ1Ј¬ЛщТФSЎчABCЈҪ![]() ЎБ2ЎБ1ЈҪ1Ј®
ЎБ2ЎБ1ЈҪ1Ј®
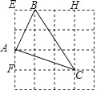
Ҫв·Ё¶юЈәҪЁБўұЯіӨОӘ1өДХэ·ҪРОНшёсЈ¬ФЪНшёсЦР»ӯіцЎчABCЈ¬К№ЎчABCИэёц¶Ҙөг¶јФЪРЎХэ·ҪРОөД¶ҘөгҙҰЈ¬ИзНј2ЛщКҫЈ¬ҪиУГНшёсГж»эҝЙөГSЎчABCЈҪSҫШРОADEC©ҒSЎчABD©ҒSЎчEBCЈҪ1Ј®
·Ҫ·ЁЗЁТЖЈәЗлҪвҙрПВГжөДОКМвЈә
ФЪЎчABCЦРЈ¬ABЎўACЎўBCИэұЯөДіӨ·ЦұрОӘ![]() Ўў
Ўў![]() Ўў
Ўў![]() Ј¬ЗуХвёцИэҪЗРОөДГж»эЈ®
Ј¬ЗуХвёцИэҪЗРОөДГж»эЈ®

Ўҫҙр°ёЎҝSЎчABCЈҪ![]() .
.
ЎҫҪвОцЎҝ
·Ҫ·ЁЗЁТЖ:ёщҫЭМвТв»ӯіцНјРО,ЎчABCөДГж»эөИУЪҫШРОEFCHөДГж»эңpИҘИэёцРЎЦұҪЗИэҪЗРОөДГж»э;ЛјО¬НШХ№:ёщҫЭМвТв»ӯіцНјРО,ЎчABCөДГж»эөИУЪҙуҫШРОөДГж»эјхИҘИэёцРЎЦұҪЗИэҪЗРОөДГж»э
ҪЁБўұЯіӨОӘ1өДХэ·ҪРОНшёсЈ¬ФЪНшёсЦР»ӯіцЎчABCЈ¬К№ЎчABCИэёц¶Ҙөг¶јФЪРЎХэ·ҪРОөД¶ҘөгҙҰЈ¬ИзНјЛщКҫЈ¬
ҪиУГНшёсГж»эҝЙөГSЎчABCЈҪSҫШРОEFCH©ҒSЎчABE©ҒSЎчAFC©ҒSЎчCBHЈҪ9©Ғ![]() ЎБ2ЎБ1©Ғ
ЎБ2ЎБ1©Ғ![]() ЎБ3ЎБ1©Ғ
ЎБ3ЎБ1©Ғ![]() ЎБ2ЎБ3ЈҪ
ЎБ2ЎБ3ЈҪ![]()

ЎҫМвДҝЎҝТӘҙУјЧЎўТТБҪГыН¬С§ЦРСЎіцТ»ГыЈ¬ҙъұн°ај¶ІОјУЙд»чұИИь. ПЦҪ«јЧЎўТТБҪГыН¬С§ІОјУЙд»чСөБ·өДіЙјЁ»жЦЖіЙПВБРБҪёцНіјЖНјЈә
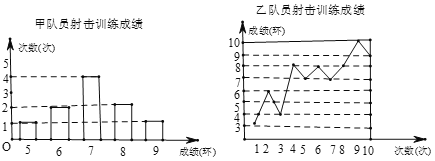
ёщҫЭТФЙПРЕПўЈ¬ХыАн·ЦОцКэҫЭИзПВЈә
ЖҪҫщіЙјЁ(»·) | ЦРО»Кэ(»·) | ЦЪКэ(»·) | ·ҪІо( | |
јЧ | 7 |
| 7 | 1. 2 |
ТТ |
| 7. 5 |
| 4. 2 |
(1)·ЦұрЗуұнёсЦР![]() Ўў
Ўў![]() Ўў
Ўў![]() өДЦө.
өДЦө.
(2)Из№ыЖдЛыІОИьСЎКЦөДЙд»чіЙјЁ¶јФЪ7»·ЧуУТЈ¬УҰёГСЎ______¶УФұІОИьёьККәПЈ»Из№ыЖдЛыІОИьСЎКЦөДЙд»чіЙјЁ¶јФЪ8»·ЧуУТЈ¬УҰёГСЎ______¶УФұІОИьёьККәП.
ЎҫМвДҝЎҝДіЧФРРіөі§Т»ЦЬјЖ»®ЙъІъ150БҫЧФРРіөЈ¬ЖҪҫщГҝМмЙъІъБҫЈ¬УЙУЪёчЦЦФӯТтКөјКГҝМмЙъІъБҝУлјЖ»®БҝПаұИУРіцИлЈ¬ПВұнКЗДіЦЬөДЙъІъЗйҝцЈЁі¬ІъОӘХэЎўјхІъОӘёәЈ©Јә
РЗЖЪ | Т» | ¶ю | Иэ | ЛД | Ое | Бщ | ИХ |
Фцјх |
|
|
|
|
|
|
|
ЈЁ1Ј©ёщҫЭјЗВјҝЙЦӘЗ°ИэМм№ІЙъІъ БҫЈ»
ЈЁ2Ј©ІъБҝЧо¶аөДТ»МмұИЙъІъБҝЧоЙЩөДТ»Мм¶аЙъІъ БҫЈ»
ЈЁ3Ј©ёГі§КөРРјЖ»®№ӨЧКЦЖЈ¬ГҝБҫіө![]() ФӘЈ¬і¬¶оНкіЙИООсГҝБҫҪұ
ФӘЈ¬і¬¶оНкіЙИООсГҝБҫҪұ![]() ФӘЈ¬ЙЩЙъІъТ»БҫҝЫ
ФӘЈ¬ЙЩЙъІъТ»БҫҝЫ![]() ФӘЈ¬ДЗГҙёГі§№ӨИЛХвТ»ЦЬөД№ӨЧКЧЬ¶оКЗ¶аЙЩЈҝ
ФӘЈ¬ДЗГҙёГі§№ӨИЛХвТ»ЦЬөД№ӨЧКЧЬ¶оКЗ¶аЙЩЈҝ
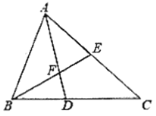
ЎҫМвДҝЎҝ№ЫІмИзНјНјРОЈ¬°СТ»ёцИэҪЗРО·ЦұрБ¬ҪУЖдИэұЯЦРөгЈ¬№№іЙ4ёцРЎИэҪЗРОЈ¬НЪИҘЦРјдөДТ»ёцРЎИэҪЗРОЈЁИзНј1Ј©Ј¬¶ФКЈПВөДИэёцРЎИэҪЗРОФЩ·ЦұрЦШёҙТФЙПЧц·ЁЈ¬ЎӯЎӯЈ¬ҫЭҙЛҪвҙрПВГжөДОКМв
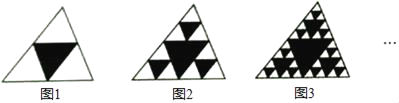
ЈЁ1Ј©МоРҙПВұнЈә
НјРО | НЪИҘИэҪЗРОөДёцКэ |
НјРО1 | 1 |
НјРО2 | 1+3 |
НјРО3 | 1+3+9 |
НјРО4 | ЎЎ ЎЎ |
ЈЁ2Ј©ёщҫЭХвёц№жВЙЈ¬ЗуНјnЦРНЪИҘИэҪЗРОөДёцКэwnЈ»ЈЁУГә¬nөДҙъКэКҪұнКҫЈ©
ЈЁ3Ј©ИфНјn+1ЦРНЪИҘИэҪЗРОөДёцКэОӘwn+1Ј¬Зуwn+1©ҒWn