题目内容
【题目】如图，在四边形ABCD中，AD＝BC，点E、F、G、H分别是AB、BD、CD、AC的中点，则四边形EFGH是（ ）
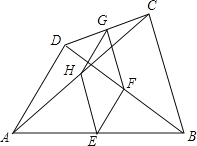
A.矩形B.菱形C.正方形D.平行四边形
【答案】B
【解析】
由题意得EF∥AD，HG∥AD，推出EF∥HG，同理得出HE∥GF，即可得出四边形EFGH是平行四边形，由中位线的性质得出GH=
AD，GF=BC，证得GH=GF，即可得出结果．
解：∵在四边形ABCD中，E、F、G、H分别是AB、BD、CD、AC的中点，
∴EF∥AD，HG∥AD，
∴EF∥HG，
同理：HE∥GF，
∴四边形EFGH是平行四边形，
∵E、F、G、H分别是AB、BD、CD、AC的中点，
∴GH＝AD，GF＝BC，
∵AD＝BC，
∴GH＝GF，
∴平行四边形EFGH是菱形；
故选B．
【题目】中秋节期间某水库养殖场为适应市场需求，连续用
天时间，采用每天降低水位以减少捕捞成本的办法．对水库中某种鲜鱼进行捕捞销售，第
天（
且为整数）的捕捞与销售的相关信息如下：
鲜鱼销售单价（元 |
|
单位捕捞成本（元 |
|
捕捞量 |
|
假定该养殖场每天捕捞和销售的鲜鱼没有损失，且能在当天全部售出．
（1）求第天的收入
（元）与（天）之间的函数关系式？（当天收入
日销售额-日捕捞成本）
（2）在第几天取得最大值，最大值是多少？
【题目】某大型水果超市销售无锡水蜜桃，根据前段时间的销售经验，每天的售价x（元/箱）与销售量y（箱）有如表关系：
每箱售价x（元） | 68 | 67 | 66 | 65 | … | 40 |
每天销量y（箱） | 40 | 45 | 50 | 55 | … | 180 |
已知y与x之间的函数关系是一次函数．
（1）求y与x的函数解析式；
（2）水蜜桃的进价是40元/箱，若该超市每天销售水蜜桃盈利1600元，要使顾客获得实惠，每箱售价是多少元？
（3）七月份连续阴雨，销售量减少，超市决定采取降价销售，所以从7月17号开始水蜜桃销售价格在（2）的条件下，下降了m%，同时水蜜桃的进货成本下降了10%，销售量也因此比原来每天获得1600元盈利时上涨了2m%（m＜100），7月份（按31天计算）降价销售后的水蜜桃销售总盈利比7月份降价销售前的销售总盈利少7120元，求m的值．
