题目内容
【题目】填空，将理由补充完整．
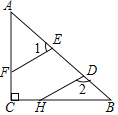
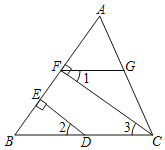
如图，CF⊥AB于F，DE⊥AB于E，∠1+∠EDC＝180°，求证：FG∥BC
证明：∵CF⊥AB，DE⊥AB（已知）
∴∠BED＝∠BFC＝90°（垂直的定义）
∴ED∥FC （ ）
∴∠2＝∠3 （ ）
∵∠1+∠EDC＝180°（已知）
又∵∠2+∠EDC＝180°（平角的定义）
∴∠1＝∠2 （ ）
∴∠1＝∠3（等量代换）
∴FG∥BC （ ）
【答案】同位角相等，两直线平行；两直线平行，同位角相等；等量代换；内错角相等，两直线平行．
【解析】
由垂直的定义得出∠BED＝∠BFC＝90°；由同位角相等得出ED∥FC；由两直线平行，同位角相等，得出∠2＝∠3；由∠1+∠EDC＝180°，∠2+∠EDC＝180°，等量代换得出∠1＝∠2，等量代换得出∠1＝∠3；由内错角相等，两直线平行即可得出结论．
证明：∵CF⊥AB，DE⊥AB（已知），
∴∠BED＝∠BFC＝90°（垂直的定义），
∴ED∥FC （同位角相等，两直线平行），
∴∠2＝∠3 （两直线平行，同位角相等），
∵∠1+∠EDC＝180°（已知），
又∵∠2+∠EDC＝180°（平角的定义），
∴∠1＝∠2 （等量代换），
∴∠1＝∠3（等量代换），
∴FG∥BC （内错角相等，两直线平行）．
故答案为：同位角相等，两直线平行；两直线平行，同位角相等；等量代换；内错角相等，两直线平行．
阅读快车系列答案
【题目】“十年树木，百年树人”，教师的素养关系到国家的未来．我市某区招聘音乐教师采用笔试、专业技能测试、说课三种形式进行选拔，这三项的成绩满分均为100分，并按2：3：5的比例折合纳入总分，最后，按照成绩的排序从高到低依次录取．该区要招聘2名音乐教师，通过笔试、专业技能测试筛选出前6名选手进入说课环节，这6名选手的各项成绩见表：
序号 | 1 | 2 | 3 | 4 | 5 | 6 |
笔试成绩 | 66 | 90 | 86 | 64 | 65 | 84 |
专业技能测试成绩 | 95 | 92 | 93 | 80 | 88 | 92 |
说课成绩 | 85 | 78 | 86 | 88 | 94 | 85 |
（1）求出说课成绩的中位数、众数；
（2）已知序号为1，2，3，4号选手的成绩分别为84.2分，84.6分，88.1分，80.8分，请你判断这六位选手中序号是多少的选手将被录用？为什么？
