题目内容
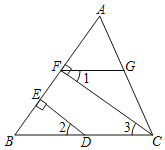
【题目】在正方形ABCD中,点E为BC边的中点,点B′与点B关于AE对称,B′B与AE交于点F,连接AB′,DB′,FC.下列结论:①AB′=AD;②△FCB′为等腰直角三角形;③∠ADB′=75°;④∠CB′D=135°.其中正确的是( )

A. ①② B. ①②④ C. ③④ D. ①②③④
【答案】B
【解析】分析:
(1)由轴对称的性质易得AB′=AB,结合AB=AD即可得到AB′=AD;
(2)连接B′E,易得BE=B′E=CE,由此易得∠BB′C=90°,由EF是△BB′C的中位线可得B′C=2EF,再证△B′EF∽△AB′F,可得![]() ,由此可得FB′=2FE,从而可得B′C=FB′,由此可得△FCB′为等腰直角三角形;
,由此可得FB′=2FE,从而可得B′C=FB′,由此可得△FCB′为等腰直角三角形;
(3)假设∠ADB′=75°成立,则可得∠AB′D=75°,由此可得∠ABB′=∠AB′B=60°,从而可得B′B=AB=BC,这与Rt△BB′C中B′B<BC矛盾,由此可得假设错误;
(4)由题意易得∠AB′D=∠ADB′,∠AB′B=∠ABB′,结合∠BAD=90°和四边形内角和为360°易得∠DB′B=135°,这样结合∠BB′C=90°可得∠DB′C=135°;
综上即可得到题中4个结论里正确的结论是①②④.
详解:
①∵点B′与点B关于AE对称,
∴△ABF与△AB′F关于AE对称,
∴AB=AB′,
∵AB=AD,
∴AB′=AD.故本选项正确;
②如图,连接EB′.

由题意可得:BE=B′E=EC,
∴∠FBE=∠FB′E,∠EB′C=∠ECB′,
∴∠FB′E+∠EB′C=∠FBE+∠ECB′=90°,
∴△BB′C为直角三角形.
∵FE为△BCB′的中位线,
∴B′C=2FE,
∵△B′EF∽△AB′F,
∴![]() ,即
,即![]() ,
,
∴FB′=2FE,
∴B′C=FB′,
∴△FCB′为等腰直角三角形.
故本选项正确.
③假设∠ADB′=75°成立,
则∠AB′D=75°,
∴∠ABB′=∠AB′B=360°-75°-75°-90°=60°,
∴△ABB′为等边三角形,
∴B′B=AB=BC,与B′B<BC矛盾,
故本选项错误.
④设∠ABB′=∠AB′B=x度,∠AB′D=∠ADB′=y度,
则在四边形ABB′D中,2x+2y+90=360,
∴x+y=135度.
又∵∠FB′C=90°,
∴∠DB′C=360°-135°-90°=135°.
故本选项正确.
故选B.

 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按x元/公里计算,耗时费按y元/分钟计算(总费用不足9元按9元计价).小明、小刚两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与打车时间如表:
时间(分钟) | 里程数(公里) | 车费(元) | |
小明 | 8 | 8 | 12 |
小刚 | 12 | 10 | 16 |
(1)求x,y的值;
(2)如果小华也用该打车方式,打车行驶了11公里,用了14分钟,那么小华的打车总费用为多少?