Question

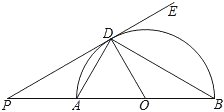
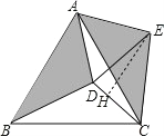
【题目】如图，在等边△ABC内有一点D，AD=5，BD=6，CD=4，将△ABD绕A点逆时针旋转，使AB与AC重合，点D旋转至点E，求∠CDE的正切值．

Answer 1

【答案】3

【解析】

先根据等边三角形的性质得AB=AC，∠BAC=60°，再根据旋转的性质得到AD=AE=5，∠DAE=∠BAC=60°，CE=BD=6，即可判定△ADE为等边三角形，得到DE=AD=5，过点E作EH⊥CD于H，如图，设DH=x,则CH=4-x,利用勾股定理得到52-x2=62-(4-x)2,解得x=，再计算出EH，然后利用正切的定义求解.

∵△ABC为等边三角形，

∴AB=AC，∠BAC=60°，

∵将△ABD绕A点逆时针旋转得到△ACE，

∴AD=AE=5，∠DAE=∠BAC=60°，CE=BD=6，

∴△ADE为等边三角形，

∴DE=AD=5，

过点E作EH⊥CD于H，如图，设DH=x,则CH=4-x,

在Rt△DHE中，EH2=52-x2

在Rt△CHE中，EH2=62-(4-x)2,

∴52-x2=62-(4-x)2,

解得x=，

∴EH=

在Rt△DHE中，tan∠CDE=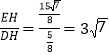

即∠CDE的正切值是