题目内容
【题目】如图,抛物线![]() 经过A(﹣1,0),B(3,0)两点,交y轴于点C,点D为抛物线的顶点,连接BD,点H为BD的中点.请解答下列问题:
经过A(﹣1,0),B(3,0)两点,交y轴于点C,点D为抛物线的顶点,连接BD,点H为BD的中点.请解答下列问题:
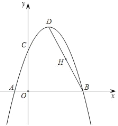
(1)求抛物线的解析式及顶点D的坐标;
(2)在y轴上找一点P,使PD+PH的值最小,则PD+PH的最小值为
【答案】(1)![]() ,D(1,4);(2) PD+PH 最小值
,D(1,4);(2) PD+PH 最小值![]()
【解析】
(1)根据题意把已知两点的坐标代入,求出b、c的值,就可以确定抛物线的解析式,配方或用公式求出顶点坐标;
(2)由题意根据B、D两点的坐标确定中点H的坐标,作出H点关于y轴的对称点点H′,连接H′D与y轴交点即为P,求出H′D即可.
解:(1)∵抛物线![]() 过点A(-1,0),B(3,0),
过点A(-1,0),B(3,0),
∴![]() ,解得
,解得![]() ,
,
∴所求函数的解析式为:![]() ,
,
化为顶点式为:![]() =-(x-1)2+4,
=-(x-1)2+4,
∴顶点D(1,4);
(2)∵B(3,0),D(1,4),
∴中点H的坐标为(2,2)其关于y轴的对称点H′坐标为(-2,2),
连接H′D与y轴交于点P,

则PD+PH最小且最小值为:![]() .
.

【题目】某工厂设计了一款成本为20元/件的工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价 | … | 30 | 40 | 50 | 60 | … |
每天销售量 | … | 500 | 400 | 300 | 200 | … |
(1)研究发现,每天销售量![]() 与单价
与单价![]() 满足一次函数关系,求出
满足一次函数关系,求出![]() 与
与![]() 的关系式;
的关系式;
(2)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润8000元?
【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,可计算出甲的平均成绩是 环(直接写出结果);
(2)已知乙的平均成绩是9环,试计算其第二次测试成绩的环数;
(3)分别计算甲、乙六次测试成绩的方差,根据计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
(计算方差的公式:![]() )
)