题目内容
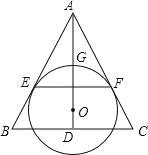
【题目】如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC 分别相切于E,F两点.
(1)证明:EF∥BC;
(2)若AG等于⊙O的半径,且AE=MN=2![]() ,求四边形EBCF的面积.
,求四边形EBCF的面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)利用等腰三角形的性质先判断AD是∠CAB的平分线,再根据切线长定理得到AE=AF,接着利用等腰三角形的性质判断AD⊥EF,然后根据平行线的判定可得到结论;
(2)先证明AD是EF的垂直平分线得到O在AD上;连结OE,OM,再根据切线的性质得到OE⊥AE,接着证明△ABC和△AEF都是等边三角形,则根据等边三角形的性质和含30度的直角三角形三边的关系计算出OE、AO,再利用勾股定理计算出OD,然后根据等边三角形的面积公式,利用四边形EBCF的面积=S△ABC-S△AEF进行计算即可.
试题解析:(1)∵△ABC是等腰三角形,AD⊥BC,
∴AD是∠CAB的平分线,
又∵☉O分别与AB,AC相切于点E,F,
∴AE=AF,
∴AD⊥EF,
∴EF∥BC;
(2)由(1)知,AE=AF,AD⊥EF,
∴AD是EF的垂直平分线,
∴O在AD上;
连结OE,OM,
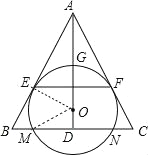
∵AB为切线,
∴OE⊥AE,
∴AG=OG=OE,
即AO=2OE,
∴∠OAE=30°,
∴∠EAF=60°,
∴△ABC和△AEF都是等边三角形,
∴AE=2![]() ,
,
∴OE=![]() AE=2,AO=2OE=4,
AE=2,AO=2OE=4,
∵OM=OE=2,DM=![]() MN=
MN=![]() ,
,
∴OD=![]() =1,
=1,
∴AD=AO+OD=5,
∴BD=![]() AD=
AD=![]() ,
,
∴AB=2BD=![]() ,
,
∴四边形EBCF的面积=S△ABC-S△AEF
=![]() (
(![]() )2-
)2-![]() ×(2
×(2![]() )2
)2
=![]() .
.

练习册系列答案
相关题目