题目内容
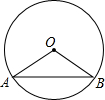 已知⊙O的半径为2,AB是它的一条弦,以0A,OB为邻边作平行四边形OAPB,若点P在⊙O上,则弦长AB为
已知⊙O的半径为2,AB是它的一条弦,以0A,OB为邻边作平行四边形OAPB,若点P在⊙O上,则弦长AB为
- A.
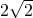
- B.

- C.3
- D.
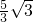
B
分析:若以0A,OB为邻边作平行四边形OAPB中,顶点P在⊙O上,那么四边形OAPB是菱形,且P是弧AB的中点;可连接OP,由垂径定理知OP垂直平分弦AB,易证得△OAP是等边三角形,即∠AOP=60°,通过解直角三角形即可得到AB的长.
解答: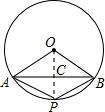 解:如图;
解:如图;
平行四边形OAPB中,OA=OB,则四边形OAPB是菱形;
若P在⊙O上,那么由AP=PB,可知P是弧AB的中点;
连接OP,则OP⊥AB,且AB=2AC=2BC;
△OAP中,OA=AP=OP,故△OAP是等边三角形,即∠AOP=60°;
Rt△OAC中,∠AOC=60°,OA=2,则AC= ,AB=2AC=2
,AB=2AC=2 ;
;
故选B.
点评:此题主要考查了平行四边形的性质、菱形的判定和性质、等边三角形的性质以及垂径定理的应用等知识,能够得到∠AOP=60°是解决问题的关键.
分析:若以0A,OB为邻边作平行四边形OAPB中,顶点P在⊙O上,那么四边形OAPB是菱形,且P是弧AB的中点;可连接OP,由垂径定理知OP垂直平分弦AB,易证得△OAP是等边三角形,即∠AOP=60°,通过解直角三角形即可得到AB的长.
解答:
 解:如图;
解:如图;平行四边形OAPB中,OA=OB,则四边形OAPB是菱形;
若P在⊙O上,那么由AP=PB,可知P是弧AB的中点;
连接OP,则OP⊥AB,且AB=2AC=2BC;
△OAP中,OA=AP=OP,故△OAP是等边三角形,即∠AOP=60°;
Rt△OAC中,∠AOC=60°,OA=2,则AC=
 ,AB=2AC=2
,AB=2AC=2 ;
;故选B.
点评:此题主要考查了平行四边形的性质、菱形的判定和性质、等边三角形的性质以及垂径定理的应用等知识,能够得到∠AOP=60°是解决问题的关键.

练习册系列答案
相关题目
已知⊙O的半径为4,A为线段PO的中点,当OP=10时,点A与⊙O的位置关系为( )
| A、在圆上 | B、在圆外 | C、在圆内 | D、不确定 |

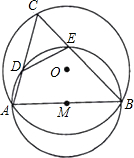 点A、点B重合).连接AC、BC,分别与⊙M相交于点D、点E,连接DE.若AB=2
点A、点B重合).连接AC、BC,分别与⊙M相交于点D、点E,连接DE.若AB=2