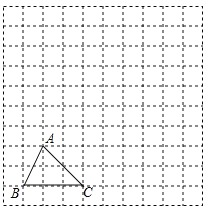Question

【题目】如图，D为△ABC的BC边上的一点，AB=10，AD=6，DC=2AD，BD= DC．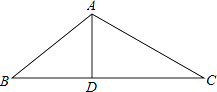
（1）求BC的长；
（2）求△ABC的面积．

Answer 1

【答案】
（1）解：∵AD=6，DC=2AD，

∴DC=12，

∵BD= DC，

∴BD=8，

BC=BD+DC=8+12=20

（2）解：在△ABD中，AB=10，AD=6，BD=8，

∵AB2=AD2+BD2，

∴△ABD为直角三角形，即AD⊥BC，

∵BC=BD+DC=8+12=20，AD=6，

∴S△ABC= ×20×6=60

【解析】（1）由DC=2AD，根据AD的长求出DC的长，进而求出BD的长即可；（2）在直角三角形ABD中，由AB，AD以及BD的长，利用勾股定理的逆定理判断得到三角形为直角三角形，即可求出三角形ABC面积．
【考点精析】解答此题的关键在于理解勾股定理的逆定理的相关知识，掌握如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形．