题目内容
【题目】如图1,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
(1)求证:△DEC≌△EDA;
(2)求DF的值;
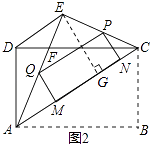
(3)如图2,若P为线段EC上一动点,过点P作△AEC的内接矩形,使其顶点Q落在线段AE上,定点M、N落在线段AC上,当线段PE的长为何值时,矩形PQMN的面积最大?并求出其最大值.
【答案】
(1)
证明:由矩形和翻折的性质可知:AD=CE,DC=EA,
在△ADE与△CED中,

∴△DEC≌△EDA(SSS)
(2)
解:如图1,
∵∠ACD=∠BAC,∠BAC=∠CAE,
∴∠ACD=∠CAE,
∴AF=CF,
设DF=x,则AF=CF=4﹣x,
在Rt△ADF中,AD2+DF2=AF2,
即32+x2=(4﹣x)2,
解得:x= ![]() ,
,
即DF= ![]()

(3)
解:如图2,由矩形PQMN的性质得PQ∥CA
∴ ![]()
又∵CE=3,AC= ![]() =5
=5
设PE=x(0<x<3),则 ![]() ,即PQ=
,即PQ= ![]()
过E作EG⊥AC于G,则PN∥EG,
∴ ![]()
又∵在Rt△AEC中,EGAC=AECE,解得EG= ![]() ,
,
∴ ![]() =
= ![]() ,即PN=
,即PN= ![]() (3﹣x),
(3﹣x),
设矩形PQMN的面积为S,
则S=PQPN=﹣ ![]() x2+4x=﹣
x2+4x=﹣ ![]()
![]() +3(0<x<3)
+3(0<x<3)
所以当x= ![]() ,即PE=
,即PE= ![]() 时,矩形PQMN的面积最大,最大面积为3.
时,矩形PQMN的面积最大,最大面积为3.
【解析】(1)由矩形和翻折的性质可知AD=CE,DC=EA,根据“SSS”可求得△DEC≌△EDA;(2)根据勾股定理即可求得.(3)由矩形PQMN的性质得PQ∥CA,所以 ![]() ,从而求得PQ,由PN∥EG,得出
,从而求得PQ,由PN∥EG,得出 ![]() ,求得PN,然后根据矩形的面积公式求得解析式,即可求得.
,求得PN,然后根据矩形的面积公式求得解析式,即可求得.
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案





