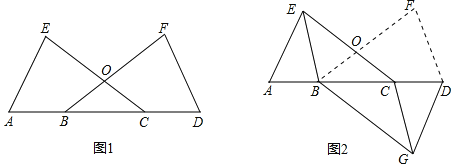题目内容
【题目】在四边形ABCD中，AD∥BC，AB=8cm，AD=16cm，BC=22cm，∠AEC=90°．点P从点A出发，以1cm/s的速度向点D运动，点Q从点C同时出发，以3cm/s的速度向点B运动，其中一个动点到达端点时，另一个动点也随之停止运动，设运动时间为t秒．
（1）当t= 时，四边形ABQP成为矩形？
（2）当t= 时，以点P、Q与点A、B、C、D中的任意两个点为顶点的四边形为平行四边形？
（3）四边形PBQD是否能成为菱形？若能，求出t的值；若不能，请说明理由，并探究如何改变Q点的速度（匀速运动），使四边形PBQD在某一时刻为菱形，求点Q的速度．
【答案】（1）
；（2）
或4；（3）四边形PBQD不能成为菱形
【解析】
试题分析：（1）由∠B=90°，AP∥BQ，由矩形的判定可知当AP=BQ时，四边形ABQP成为矩形；
（2）由（1）可求得点P、Q与点A、B为顶点的四边形为平行四边形；然后由当PD=CQ时，CDPQ是平行四边形，求得t的值；
（3）由PD∥BQ，当PD=BQ=BP时，四边形PBQD能成为菱形，先由PD=BQ求出运动时间t的值，再代入求BP，发现BP≠PD，判断此时四边形PBQD不能成为菱形；设Q点的速度改变为vcm/s时，四边形PBQD在时刻t为菱形，根据PD=BQ=BP列出关于v、t的方程组，解方程组即可求出点Q的速度．
解：（1）如图1，∵∠B=90°，AP∥BQ，
∴当AP=BQ时，四边形ABQP成为矩形，
此时有t=22﹣3t，解得t=．
∴当t=时，四边形ABQP成为矩形；
故答案为：；
（2）如图1，当t=时，四边形ABQP成为矩形，
如图2，当PD∥CQ时，四边形CDPQ是平行四边形，
则16﹣t=3t，
解得：t=4，
∴当t=或4时，以点P、Q与点A、B、C、D中的任意两个点为顶点的四边形为平行四边形；
故答案为：或4；
（3）四边形PBQD不能成为菱形．理由如下：
∵PD∥BQ，
∴当PD=BQ=BP时，四边形PBQD能成为菱形．
由PD=BQ，得16﹣t=22﹣3t，
解得：t=3，
当t=3时，PD=BQ=13，BP=
=
=
=
≠13，
∴四边形PBQD不能成为菱形；
如果Q点的速度改变为vcm/s时，能够使四边形PBQD在时刻ts为菱形，
由题意，得
，解得
．
故点Q的速度为2cm/s时，能够使四边形PBQD在某一时刻为菱形．
