题目内容
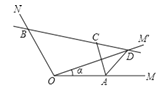
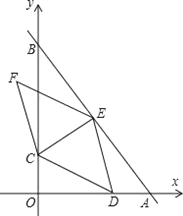
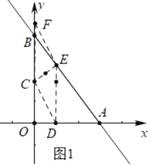
【题目】如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于A(12,0),B(0,16),点C从B点出发向y轴负方向以每秒2个单位的速度运动,过点C作CE⊥AB于点E,点D为x轴上动点,连结CD,DE,以CD,DE为边作CDEF.设运动时间为t秒.
(1)求点C运动了多少秒时,点E恰好是AB的中点?
(2)当t=4时,若CDEF的顶点F恰好落在y轴上,请求出此时点D的坐标;
(3)点C在运动过程中,若在x轴上存在两个不同的点D使CDEF成为矩形,求出满足条件的t的取值范围.
【答案】(1)点C运动了6.25秒时,点E恰好是AB的中点;(2)D(![]() ,0);(3)
,0);(3)![]()
【解析】
(1)在Rt△AOC中,利用勾股定理构建方程即可解决问题;
(2求出直线CE解析式,利用方程组确定点E坐标即可解决问题;
(3)求出两个特殊位置的时间t即可解决问题.①当点C在y轴的正半轴上时,设以EC为直径的⊙P与x轴相切于点D,作ER⊥OA于R.求出此时的时间t;
②当点C′在y轴的负半轴上时,设以E′C′为直径的⊙P′与x轴相切于点D′,作E′K⊥OA于K.求出此时的时间t;
(1)根据题意知BC=2t、BO=16、OA=12,则OC=16﹣2t,
∵CE⊥AB且E为AB中点,∴CB=CA=2t,
在Rt△AOC中,由OC2+OA2=AC2可得(16﹣2t)2+122=(2t)2,解得:t=6.25,
即点C运动了6.25秒时,点E恰好是AB的中点;
(2)如图1中, 当t=4时,BC=OC=8,∵A(12,0),B(0,16),
∴直线AB的解析式为y=﹣![]() x+16,∵CE⊥AB,C(0,8),∴直线CE的解析式为y=
x+16,∵CE⊥AB,C(0,8),∴直线CE的解析式为y=![]() x+8,
x+8,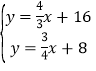 ,解得
,解得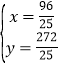 ,∴E(
,∴E(![]() ,
,![]() ),∵点F在y轴上,∴DE∥y轴,∴D(
),∵点F在y轴上,∴DE∥y轴,∴D(![]() ,0).
,0).
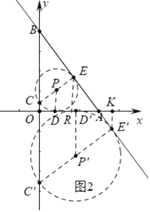
(3)如图2中,
①当点C在y轴的正半轴上时,设以EC为直径的⊙P与x轴相切于点D,作ER⊥OA于R.
根据PD=![]() (OC+ER),可得:
(OC+ER),可得:![]() t=
t=![]() [16﹣2t+(20﹣
[16﹣2t+(20﹣![]() t)×
t)×![]() ],解得t=
],解得t=![]() .
.
②当点C′在y轴的负半轴上时,设以E′C′为直径的⊙P′与x轴相切于点D′,作E′K⊥OA于K.
根据P′D′=![]() (OC′+E′K),可得:
(OC′+E′K),可得:![]() t=
t=![]() [2t﹣16+(
[2t﹣16+(![]() t﹣20)×
t﹣20)×![]() ],解得t=
],解得t=![]() ,
,
综上所述,点C在运动过程中,若在x轴上存在两个不同的点D使CDEF成为矩形,满足条件的t的取值范围为![]() <t<
<t<![]() .
.

 名校通行证有效作业系列答案
名校通行证有效作业系列答案【题目】A城有肥料200吨,B城有肥料300吨.现要把这些肥料全部运往C,D两乡,从A城往C,D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C,D两乡运肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.设从A城调往C乡肥料x吨.
(1)根据题意,填写下表:
调入地 数量/吨 调出地 | C | D |
A | x | ______ |
B | _____ | ______ |
总计 | 240 | 260 |
(2)给出完成此项调运任务最节省费用的调运方案及所需费用,并说明理由.