题目内容
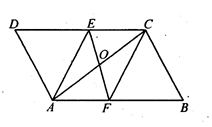
如图,在菱形ABCD中,∠A=100°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC=


| A.35° | B.45° | C.50° | D.55° |
C
试题分析:延长EF交DC的延长线于H点.证得△BEF≌△CHF,可得EF=FH.在Rt△PEH中,利用直角三角形的性质,可得∠FPC=∠FHP=∠BEF,在等腰△BEF中即可求得求∠BEF的度数.
延长EF交DC的延长线于H点

∵在菱形ABCD中,∠A=100°,E,F分别是边AB和BC的中点
∴∠B=80°,BE=BF
∴∠BEF=(180°-80°)÷2=50°
∵AB∥DC
∴∠FHC=∠BEF=50°
又∵BF=FC,∠B=∠FCH
∴△BEF≌△CHF
∴EF=FH
∵EP⊥DC
∴∠EPH=90°
∴FP=FH
∴∠FPC=∠FHP=∠BEF=50°.
故选C.
点评:解答本题的关键是读懂题意及图形,正确作出辅助线,熟练运用直角三角形斜边上的中线等于斜边的一半解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



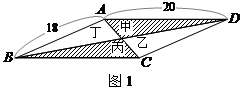
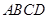 的面积为120,
的面积为120,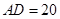 ,
,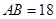 .沿两对角线将四边形
.沿两对角线将四边形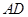 、
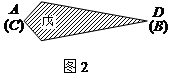
、 重合)形成对称图形戊,如图2所示,则图形戊的两条对角线长度之和是 .
重合)形成对称图形戊,如图2所示,则图形戊的两条对角线长度之和是 .