题目内容
【题目】如图1,点O是弹力墙MN上一点,魔法棒从OM的位置开始绕点O向ON的位置顺时针旋转,当转到ON位置时,则从ON位置弹回,继续向OM位置旋转;当转到OM位置时,再从OM的位置弹回,继续转向ON位置,…,如此反复.按照这种方式将魔法棒进行如下步骤的旋转:第1步,从OA0(OA0在OM上)开始旋转α至OA1;第2步,从OA1开始继续旋转2α至OA2;第3步,从OA2开始继续旋转3α至OA3 , ….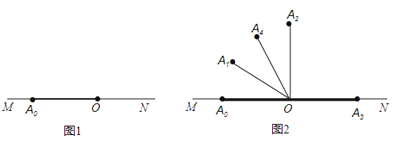
例如:当α=30°时,OA1 , OA2 , OA3 , OA4的位置如图2所示,其中OA3恰好落在ON上,∠A3OA4=120°;
当α=20°时,OA1 , OA2 , OA3 , OA4 , OA3的位置如图3所示,
其中第4步旋转到ON后弹回,即∠A3ON+∠NOA4=80°,而OA3恰好与OA2重合.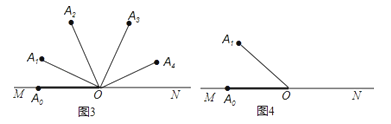
![]()
(1)若α=35°,在图4中借助量角器画出OA2 , OA3 , 其中∠A3OA2的度数是 ;
(2)若α<30°,且OA4所在的射线平分∠A2OA3 , 在如图5中画出OA1 , OA2 , OA3 , OA4并求出α的值
(3)若α<36°,且∠A2OA4=20°,则对应的α值是
(4)当OAi所在的射线是∠AiOAk(i,j,k是正整数,且OAj与OAk不重合)的平分线时,旋转停止,请探究:试问对于任意角α(α的度数为正整数,且α=180°),旋转是否可以停止?写出你的探究思路.
【答案】
(1)![]()
(2)
解:如图所示
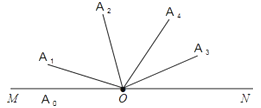
∵α<30°,
∴∠A0OA3<180°,4α<180°.
∵OA4平分∠A2OA3,
∴2(180°﹣6α)+![]() =4α,解得:
=4α,解得:![]() .
.
(3)![]()
(4)
解:对于角α=120°不能停止.理由如下:
无论a为多少度,旋转过若干次后,一定会出现OAi是∠AiOAK是的角平分线,所以旋转会停止.
但特殊的,当a为120°时,第一次旋转120°,∠MOA1=120°,第二次旋转240°时,与OM重合,第三次旋转360°,又与OM重合,第四次旋转480°时,又与OA1重合,…依此类推,旋转的终边只会出现“与OM重合”或“与OA1重合”两种情况,不会出第三条射线,所以不会出现OAi是∠AiOAK是的角平分线这种情况,旋转不会停止.
【解析】(1)根据题意,明确每次旋转的角度,计算即可;
(2)根据各角的度数,找出等量关系式,列出方程,求出α的度数即可;
(3)类比第(2)小题的算法,分三种情况讨论,求出α的度数即可;
(4)无论a为多少度,旋转很多次,总会出一次OAi是∠AiOAK是的角平分线,但当a=120度时,只有两条射线,不会出现OAi是∠AiOAK是的角平分线,所以旋转会中止.