题目内容
【题目】如图,已知△ABC中,AB=AC,BD,CE是高,BD与CE相交于点O 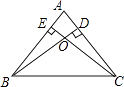
(1)求证:OB=OC;
(2)若∠ABC=50°,求∠BOC的度数.
【答案】
(1)证明:∵AB=AC,
∴∠ABC=∠ACB,
∵BD、CE是△ABC的两条高线,
∴∠BEC=∠BDE=90°
∴△BEC≌△CDB
∴∠DBC=∠ECB,BE=CD
在△BOE和△COD中
∵∠BOE=∠COD,BE=CD,∠BEC=∠BDE=90°
∴△BOE≌△COD,
∴OB=OC
(2)∵∠ABC=50°,AB=AC,
∴∠A=180°﹣2×50°=80°,
∴∠DOE+∠A=180°
∴∠BOC=∠DOE=180°﹣80°=100°
【解析】(1)首先根据等腰三角形的性质得到∠ABC=∠ACB,然后利用高线的定义得到∠ECB=∠DBC,从而得证;(2)首先求出∠A的度数,进而求出∠BOC的度数.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
