题目内容
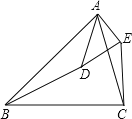
【题目】如图,在平行四边形![]() 中,过点
中,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,
,![]() 为
为![]() 上一点,且
上一点,且![]() .
.
(1)求证:![]() .
.
(2)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
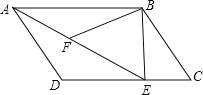
【答案】(1)见解析;(2)![]()
【解析】
(1)求三角形相似就要得出两组对应的角相等,已知了∠BFE=∠C,根据等角的补角相等可得出∠ADE=∠AFB,根据AB∥CD可得出∠BAF=∠AED,这样就构成了两三角形相似的条件.
(2)根据(1)的相似三角形可得出关于AB,AE,AD,BF的比例关系,有了AD,AB的长,只需求出AE的长即可.可在直角三角形ABE中用勾股定理求出AE的长,这样就能求出BF的长了.
(1)证明:在平行四边形ABCD中,
∵∠D+∠C=180°,AB∥CD,
∴∠BAF=∠AED.
∵∠AFB+∠BFE=180°,∠D+∠C=180°,∠BFE=∠C,
∴∠AFB=∠D,
∴△ABF∽△EAD.
(2)解:∵BE⊥CD,AB∥CD,
∴BE⊥AB.
∴∠ABE=90°.
∴![]() .
.
∵△ABF∽△EAD,
![]() ,
,
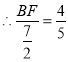 .
.
![]() .
.

练习册系列答案
相关题目
【题目】某农科所在相同条件下做某作物种子发芽率的实验,结果如下表所示:
种子个数 | 200 | 300 | 500 | 700 | 800 | 900 | 1000 |
发芽种子个数 | 187 | 282 | 435 | 624 | 718 | 814 | 901 |
发芽种子率 | 0.935 | 0.940 | 0.870 | 0.891 | 0.898 | 0.904 | 0.901 |
下面有四个推断:
①种子个数是700时,发芽种子的个数是624,所以种子发芽的概率是0.891;
②随着参加实验的种子数量的增加,发芽种子的频率在0.9附近摆动,显示出一定的稳定性,可以估计种子发芽的概率约为0.9(精确到0.1);
③实验的种子个数最多的那次实验得到的发芽种子的频率一定是种子发芽的概率;
④若用频率估计种子发芽的概率约为0.9,则可以估计![]() 种子中大约有
种子中大约有![]() 的种子不能发芽.
的种子不能发芽.
其中合理的是______.