题目内容
如图2,已知AD是△ABC的中线,AE=EF=FC,下面给出三个关系式: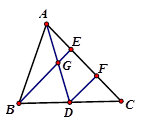
①AG:AD=1:2; ②GE:BE=1:3 ③BE:BG=4:3,
其中正确的是( )
| A.①② | B.①③ | C.②③ | D.①②③ |
B.
解析试题分析:AD是△ABC的中线,AE=EF=FC,所以DF为三角形BEC的中位线,所以DF∥BE且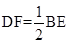 ,GE为三角形ADF的中位线EG∥DF, 且
,GE为三角形ADF的中位线EG∥DF, 且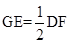 ,所以①AG:AD="1:2" ③BE:BG=4:3,正确GE:BE=1:4,②GE:BE=1:3错误,故选B.
,所以①AG:AD="1:2" ③BE:BG=4:3,正确GE:BE=1:4,②GE:BE=1:3错误,故选B.
考点:三角形的中位线.

练习册系列答案
相关题目
如图,△ABC中,AB>AC,D为AB上一点,下列条件:①∠B=∠ACD,②∠ADC=∠ACB,③ ,④
,④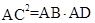 中,能判定△ABC与△ACD相似的有( )
中,能判定△ABC与△ACD相似的有( )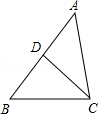
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,将矩形纸片ABCD沿EF折叠,使点B与CD的中点重合,若AB=2,BC=3,则△FCB′与△B′DG的面积之比为( )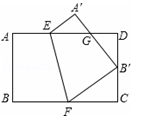
| A.3:2 | B.9:4 | C.4:3 | D.16:9 |
设 是三个互不相同的正数,如果
是三个互不相同的正数,如果 ,那么( )
,那么( )
A. | B. | C. | D.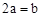 |
下列四组数中,能组成比例的是( ).
A. , , , , , , ; ; | B. , , , , , , ; ; |
C. , , , , , , ; ; | D. , , , , , , . . |
 (非直径)为对称轴将
(非直径)为对称轴将 折叠后与
折叠后与 相交于点
相交于点 ,如果
,如果 ,那么
,那么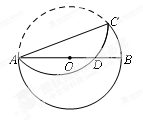




 AE,垂足为G,BG=
AE,垂足为G,BG=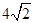 ,则△CEF的周长为( )
,则△CEF的周长为( )
 中,点D、E分别在边AB 、AC上,下列比例式不能判定
中,点D、E分别在边AB 、AC上,下列比例式不能判定 ∥
∥ 的是( ).
的是( ).
 ; B.
; B. ;C.
;C. ;D.
;D. .
. (
( 均不为0),则
均不为0),则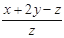 的值为 .
的值为 .