题目内容
某学生参加社会实践活动,在景点P处测得景点B位于南偏东45°方向,然后沿北偏东60°方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之间的距离.
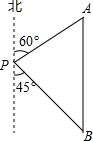

过P作PD⊥AB,垂足为D,则AB=AD+BD,
由题意,得∠A=60,∠APD=30,且PA=100米,
∴AD=50米,
又∵∠B=∠DPB=45°,
∴DB=DP,
∵DP=
=50
(米),
∴AB=50+50
(米).
∴景点A与景点B之间的距离为(50+50
)米.

由题意,得∠A=60,∠APD=30,且PA=100米,
∴AD=50米,
又∵∠B=∠DPB=45°,
∴DB=DP,
∵DP=
| 1002-502 |
| 3 |
∴AB=50+50
| 3 |
∴景点A与景点B之间的距离为(50+50
| 3 |


练习册系列答案
相关题目