题目内容
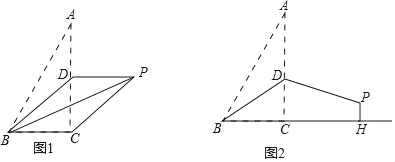
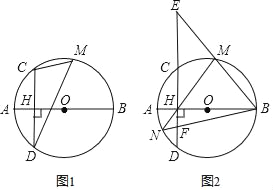
【题目】如图1,线段AB是圆O的直径,弦CD⊥AB于点H,点M是弧CBD上任意一点,AH=4,CD=16.
(1)求圆O的半径r的长度;
(2)求tan∠CMD;
(3)如图2,直径BM交直线CD于点E,直线MH交圆O于点N,连接BN交CE于点F,求HEHF的值.
【答案】(1)圆O的半径r的长度为10;(2)tan∠CMD=![]() ;(3)HEHF的值为64.
;(3)HEHF的值为64.
【解析】
(1)在Rt△COH中,利用勾股定理即可解决问题;
(2)只要证明∠CMD=∠COA,求出tan∠COA即可;
(3)由△EHM∽△NHF,推出HEHF=HMHN,又HMHN=AHHB,推出HEHF=AHHB,由此即可解决问题
(1)如图1中,连接OC.
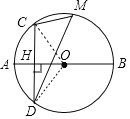
∵AB⊥CD,∴∠CHO=90°,
在Rt△COH中,∵OC=r,OH=r-4,CH=4,
∴r2=42+(r-4)2,∴r=10.
答:圆O的半径r的长度为10;
(2)如图1中,连接OD.
∵AB⊥CD,AB是直径,
∠COA=![]() ,∠M=
,∠M=![]() ,
,
∴∠COA=∠CMD,
∴tan∠CMD=tan∠COA=![]() ;
;
(3)如图2中,连接AM.
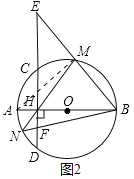
∵AB是直径,
∴∠AMB=90°,
∴∠MAB+∠ABM=90°,
∵∠E+∠ABM=90°,
∴∠E=∠MAB,
∴∠MAB=∠MNB=∠E,
∵∠EHM=∠NHF
∴△EHM∽△NHF,
∴HEHF=HMHN,
∵HMHN=AHHB,
∴HEHF=AHHB=164=64.
答:HEHF的值为64.

【题目】已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:
x | -1 | 0 | 1 | 3 |
y | -3 | 1 | 3 | 1 |
下列结论:①抛物线的开口向下;②其图象的对称轴为x=1;③当x<1时,函数值y随x的增大而增大;④方程ax2+bx+c=0有一个根大于4,其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个