Question

【题目】阅读下列材料，然后解答后面的问题．

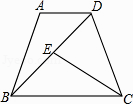
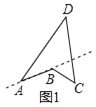
（1）定义：把四边形的某些边向两方延长，其他各边有不在延长所得直线的同一旁，这样的四边形叫做凹四边形．如图1，四边形ABCD为凹四边形．

（2）性质探究：请完成凹四边形一个性质的证明．

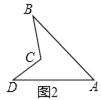
已知：如图2，四边形ABCD是凹四边形．

求证：∠BCD=∠B+∠A+∠D．

（3）性质应用：

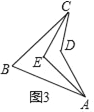
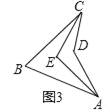
如图3，在凹四边形ABCD中，∠BAD的角平分线与∠BCD的角平分线交于点E，若∠ADC=140°，∠AEC=102°，则∠B=_____°．

Answer 1

【答案】64

【解析】

（2）延长BC交AD于点M，根据三角形的外角的性质即可解决问题．
（3）利用（2）中结论如图3中，设∠B=x，∠ECB=∠ECD=α，∠EAD=∠EAB=β，列出方程组即可解决问题．

（2）延长BC交AD于点M

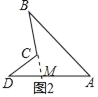
∵∠BCD是△CDM的外角，

∴∠BCD=∠CMD+∠D，

同理∠CD是△ABM的外角，

∴∠CMD=∠A+∠B，

∴∠BCD=∠A+∠B+∠D；

（3）如图3中，设∠B=x，∠ECB=∠ECD=α，∠EAD=∠EAB=β．

由（2）可知， ，

解得x=64°

故答案为64．