题目内容
【题目】某船向正东航行,在A处望见灯塔C在东北方向,前进到B处望见灯塔C在北偏西30°,又航行了半小时到D处,望见灯塔C恰在西北方向,若船速为每小时20海里.求A、D两点间的距离.(结果不取近似值)
【答案】解:作CH⊥AD于点H,
由题意可得:△ACD是等腰直角三角形,则CH= ![]() AD,设CH=x,则DH=x,
AD,设CH=x,则DH=x,
在Rt△CBH中,∠BCH=30°,
则 ![]() =tan30°,故BH=
=tan30°,故BH= ![]() x,
x,
∴BD=x﹣ ![]() x=
x= ![]() ×20,
×20,
解得:x=15+5 ![]() ,
,
故2x=30+10 ![]() .
.
答:A、D两点间的距离为(30+10 ![]() )海里.
)海里.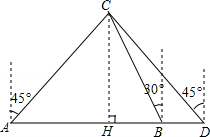
【解析】先作CH⊥AD,可得BD= ![]() ×20,AH=DH,可求AH的长,从而求得AD的长.
×20,AH=DH,可求AH的长,从而求得AD的长.
【考点精析】关于本题考查的关于方向角问题,需要了解指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角才能得出正确答案.

练习册系列答案
相关题目