Question

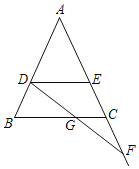
【题目】如图，在△ABC中，AB＝AC．点D，E分别在AB，AC边上，点F在AC边的延长线上，且BD＝CE＝CF．

（1）连接DE，判断DE与BC的位置关系，为什么？

（2）连接DF交BC于点G．判断DG与GF的数量关系，并说明理由．

Answer 1

【答案】（1）DE∥BC，DG＝GF，见解析；（2）DG＝GF，见解析.

【解析】

（1）利用等腰三角形的性质证明∠ADE＝∠B即可解决问题；

（2）利用平行线等分线段定理即可解决问题；

解：（1）结论：DE∥BC．

理由：∵AB＝AC，

∴∠B＝∠ACB，

∵BD＝EC，

∴AD＝AE，

∴∠ADE＝∠AED，

∵∠A+2∠ADE＝180°，∠A+2∠B＝180°，

∴∠ADE＝∠B，

∴DE∥BC．

（2）结论：DG＝GF．

理由：∵CG∥DE，EC＝CF，

∴DG＝GC．