Question

【题目】在平面直角坐标系中，抛物线经过点，.

（1）求该抛物线的函数表达式及对称轴；

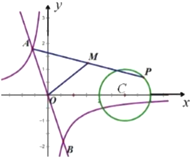
（2）设点关于原点的对称点为，点是抛物线对称轴上一动点，记抛物线在，之间的部分为图象（包含，两点），如果直线与图象有一个公共点，结合函数的图象，直接写出点纵坐标的取值范围.

Answer 1

【答案】（1）抛物线的表达式为，抛物线的对称轴为；（2）或.

【解析】

(1)将点A、B代入利用待定系数法解出即可.

(2)由题意确定C坐标,以及二次函数的最小值,确定出D纵坐标的最小值,求直线AC解析式,令x=1求出y的值,由对称性即可得范围.

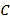
解：（1）∵点，在抛物线上，

∴

解得

∴抛物线的表达式为.

∴抛物线的对称轴为.

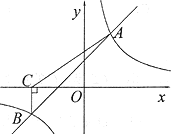
（2）由题意得:C(-3,4),二次函数的最大值为4.

设直线AC:y=kx+b,

将点A和C代入得:,解得: .

∴直线AC的表达式为.

当x=1时, .

由对称性可知,此时与BC交点的纵坐标为: .

∴点D纵坐标t的范围为:或.