题目内容
【题目】某基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长54米的不锈钢栅栏围成,与墙平行的一边留一个宽为2米的出入口,如图所示,如何设计才能使园地的而积最大?下面是两位学生争议的情境:请根据上面的信息,解决问题:

(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
(2)请你判断谁的说法正确,为什么?
【答案】(1)、BC=56-2x;(2)、小娟的说法正确;理由见解析
【解析】
试题分析:(1)、BC的长度=围栏的长度-AB和CD的长度+门的宽度;(2)、首先求出S和x的二次函数关系,然后根据二次函数的性质求出S取最大值时x的值,从而得出矩形不是正方形.
试题解析:(1)、设AB=x米,可得BC=54﹣2x+2=56﹣2x;
(2)、小娟的说法正确;
矩形面积S=x(56﹣2x)=﹣2(x﹣14)2+392,
∵56﹣2x>0,
∴x<28,
∴0<x<28,
∴当x=14时,S取最大值,
此时x![]() 56﹣2x,
56﹣2x,
∴面积最大的不是正方形.

练习册系列答案
相关题目
【题目】2013年5月23日起,我市将对行人闯红灯分三档进行处罚,九年级数学研究学习小组在某十字路口随机调查部分市民对该法归的了解情况,统计结果后绘制了如图的三副不完整的统计图,请结合图中相关数据回答下列问题.
得分 | |||||||
A | 50<n≤60 | ||||||
B | 60<n≤70 | ||||||
C | 70<n≤80 | ||||||
D | 80<n≤90 | ||||||
E | 90<n≤100 | ||||||
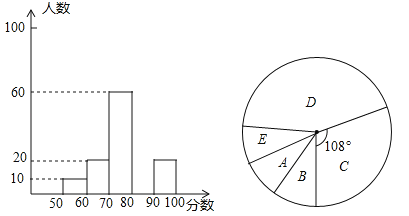
(1)本次共调查的人数为 ;
(2)补全频数分布图;
(3)在扇形统计图中,“B”所在的扇形的圆心角的度数为 ;
(4)若在这一周里,该路口共有2000人通过,则可估计得分在80以上的人数大约为 .