题目内容
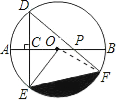
【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连结EF、EO,若DE=![]() ,∠DPA=45°.
,∠DPA=45°.
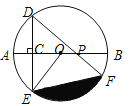
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
【答案】(1)2;(2)![]() .
.
【解析】试题分析:(1)根据垂径定理得CE的长,再根据已知DE平分AO得CO=![]() AO=
AO=![]() OE,解直角三角形求解.
OE,解直角三角形求解.
(2)先求出扇形的圆心角,再根据扇形面积和三角形的面积公式计算即可.
试题解析:(1)∵直径AB⊥DE,∴CE=![]() DE=
DE=![]() .∵DE平分AO,∴CO=
.∵DE平分AO,∴CO=![]() AO=
AO=![]() OE.又∵∠OCE=90°,∴sin∠CEO=
OE.又∵∠OCE=90°,∴sin∠CEO=![]() =
=![]() ,∴∠CEO=30°.在Rt△COE中,OE=
,∴∠CEO=30°.在Rt△COE中,OE=![]() =
=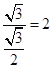 .∴⊙O的半径为2.
.∴⊙O的半径为2.
(2)连接OF.在Rt△DCP中,∵∠DPC=45°,∴∠D=90°﹣45°=45°.∴∠EOF=2∠D=90°.∴S扇形OEF=![]() .∵∠EOF=2∠D=90°,OE=OF=2,∴SRt△OEF=
.∵∠EOF=2∠D=90°,OE=OF=2,∴SRt△OEF=![]() ×OE×OF=2.∴S阴影=S扇形OEF﹣SRt△OEF=
×OE×OF=2.∴S阴影=S扇形OEF﹣SRt△OEF=![]() .
.

练习册系列答案
相关题目
【题目】科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如下表):
温度 | …… | -4 | -2 | 0 | 2 | 4 | 4.5 | …… |
植物每天高度增长量 | …… | 41 | 49 | 49 | 41 | 25 | 19.75 | …… |
这些数据说明:植物每天高度增长量![]() 关于温度
关于温度![]() 的函数是反比例函数、一次函数和二次函数中的一种.
的函数是反比例函数、一次函数和二次函数中的一种.
(1)你认为是哪一种函数,并求出它的函数关系式;
(2)温度为多少时,这种植物每天高度增长量最大?
(3)如果实验室温度保持不变,在10天内要使该植物高度增长量的总和超过250mm,那么实验室的温度![]() 应该在哪个范围内选择?请直接写出结果.
应该在哪个范围内选择?请直接写出结果.