题目内容
【题目】△![]() 中,
中, ![]() .取
.取![]() 边的中点
边的中点![]() ,作
,作![]() ⊥
⊥![]() 于点
于点![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() 交于点
交于点![]() .
.
(1)如图1,如果![]() ,求证:
,求证: ![]() ⊥
⊥![]() 并求
并求![]() 的值;
的值;
(2)如图2,如果![]() ,求证:
,求证: ![]() ⊥
⊥![]() 并用含
并用含![]() 的式子表示
的式子表示![]() .
.

【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:连接AD,根据等腰三角形的性质可得∠ABC=∠C,∠BAD=![]() ∠BAC,AD⊥BC,然后根据同角的余角相等可得∠ADE=∠C.易证△ADB∽△DEC,可得ADCE=BDDE.由此可得ADCE=
∠BAC,AD⊥BC,然后根据同角的余角相等可得∠ADE=∠C.易证△ADB∽△DEC,可得ADCE=BDDE.由此可得ADCE=![]() BC2DF=BCDF,即
BC2DF=BCDF,即![]() ,由此可证到△AFD∽△BEC,则有
,由此可证到△AFD∽△BEC,则有![]() ,在Rt△ADB中根据三角函数的定义可得tan∠ABD=tan(90°-
,在Rt△ADB中根据三角函数的定义可得tan∠ABD=tan(90°-![]() ∠BAC)=
∠BAC)=![]() ,从而可得
,从而可得![]() =
=![]() tan(90°-
tan(90°-![]() ∠BAC).由△AFD∽△BEC可得∠DAF=∠CBE,即可得到∠DAF+∠AOH=∠CBE+∠BOD=90°,即可得到∠AHB=90°.利用以上结论即可解决题中的两个问题.
∠BAC).由△AFD∽△BEC可得∠DAF=∠CBE,即可得到∠DAF+∠AOH=∠CBE+∠BOD=90°,即可得到∠AHB=90°.利用以上结论即可解决题中的两个问题.
试题解析:如图1,连接AD,
∵AB=AC,点D是BC的中点,
∴∠ABC=∠C,∠BAD=∠DAC=![]() ∠BAC,AD⊥BC,
∠BAC,AD⊥BC,
∵AD⊥BC,DE⊥AC,
∴∠ADE+∠CDE=90°,∠C+∠CDE=90°,
∴∠ADE=∠C.
又∵∠ADB=∠DEC=90°,
∴△ADB∽△DEC,
∴![]() ,
,
即ADCE=BDDE.
∵点D是BC的中点,点F是DE的中点,
∴BD=![]() BC,DE=2DF,
BC,DE=2DF,
∴ADCE═![]() BC2DF=BCDF,
BC2DF=BCDF,
∴![]() ,
,
又∵∠ADE=∠C,
∴△AFD∽△BEC,
∴![]() ,
,
在Rt△ADB中,
∵∠ABD=90°-∠BAD=90°-![]() ∠BAC,BD=
∠BAC,BD=![]() BC,
BC,
∴tan∠ABD=tan(90°-![]() ∠BAC)=
∠BAC)=![]() ,
,
∴![]() =
=![]() tan(90°-
tan(90°-![]() ∠BAC).
∠BAC).
∵△AFD∽△BEC,
∴∠DAF=∠CBE.
∵∠CBE+∠BOD=90°,∠AOH=∠BOD,
∴∠DAF+∠AOH=∠CBE+∠BOD=90°,
∴∠AHO=180°-90°=90°,即∠AHB=90°,
(1)如图1,
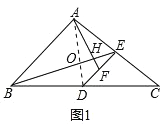
根据以上结论可得:
∠AHB=90°,![]() =
=![]() tan(90°-
tan(90°-![]() ×90°)=
×90°)=![]() ;
;
∴AF⊥BE, ![]() =
=![]() ;
;
(2)如图2,
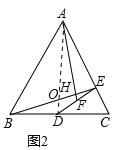
根据以上结论可得:∠AHB=90°,![]() =
=![]() tan(90°-
tan(90°-![]() α);
α);
∴AF⊥BE, ![]() =
=![]() tan(90°-
tan(90°-![]() α).
α).

 活力课时同步练习册系列答案
活力课时同步练习册系列答案