题目内容
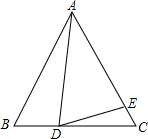
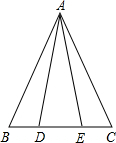
如图,在△ABC中,∠B=60°,AB=12cm,BC=4cm,现有一动点P从点A出发,以2cm/秒的速度沿射线AB运动,试回答下列问题:
(1)运动几秒时△PBC为等腰三角形?
(2)运动几秒时△PBC为直角三角形?
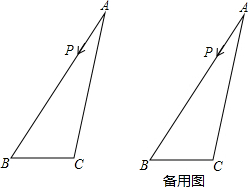
(1)运动几秒时△PBC为等腰三角形?
(2)运动几秒时△PBC为直角三角形?

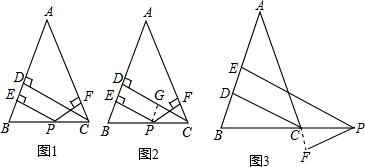
(1)当点P在线段AB上时,如图1,
∵∠B=60°,△PBC为等腰三角形,
∴△PBC是等边三角形,
∴PB=BC=4cm,
AP=AB-BP=12-4=8cm,
∴运动时间为:8÷2=4秒,;
当点P在线段AB外时,如图1,
∵∠PC=120°,
∴BP=BC=4,
∴此时,PB=AB+BP=12+4=16,
∴时间等于16除以2等于8s.
故运动4秒时△PBC为等腰三角形;
(2)∠BCP=90°时,BP=2BC=2×4=8cm,
∴AP=AB-BP=12-8=4cm,
运动时间为:4÷2=2秒,
∠BPC=90°时,BP=
BC=
×4=2cm,
∴AP=AB-BP=12-2=10cm,
∴运动时间为:10÷2=5秒,
故运动2秒或5秒时△PBC为直角三角形.

∵∠B=60°,△PBC为等腰三角形,
∴△PBC是等边三角形,
∴PB=BC=4cm,
AP=AB-BP=12-4=8cm,
∴运动时间为:8÷2=4秒,;
当点P在线段AB外时,如图1,
∵∠PC=120°,
∴BP=BC=4,
∴此时,PB=AB+BP=12+4=16,
∴时间等于16除以2等于8s.
故运动4秒时△PBC为等腰三角形;
(2)∠BCP=90°时,BP=2BC=2×4=8cm,
∴AP=AB-BP=12-8=4cm,
运动时间为:4÷2=2秒,
∠BPC=90°时,BP=
| 1 |
| 2 |
| 1 |
| 2 |
∴AP=AB-BP=12-2=10cm,
∴运动时间为:10÷2=5秒,
故运动2秒或5秒时△PBC为直角三角形.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目